X7: Utilizing Libraries

Abstraction is the process of ignoring minutiae and focusing on the big picture. In modern life, we are constantly confronted with objects much too complex to be understood by the average person. For example, to really grasp how a television works, one must have extensive knowledge of electrical engineering, electronics, and physics. However, most people watch and operate television sets every day. This is possible because they abstract away unnecessary details and focus on the features relevant to their needs — it is a box with several inputs (power cord, on/off button, channel selector, and volume control) and two outputs (picture and sound). This degree of understanding enables them to watch and have control over the television set without knowing the specifics of television's functionality.

You have already been introduced to the idea of abstraction in programming through the use of functions. In a programming language, a function represents a unit of computation from which the details are abstracted away. For example, the computation involved in finding the square root of a number is certainly not trivial, but the Math.sqrt function encapsulates this multistep process in a single function call. Without worrying about how it computes the square root, a programmer can call the function and use it to obtain a result. In this chapter, you will learn to define and use your own full-featured functions and incorporate them into your Web pages. In addition, you will learn to utilize libraries of functions so that general-purpose abstractions can be defined once and used repeatedly.

      General-purpose Functions

In Chapter X5, you learned how to create user-defined functions to simplify the body of a Web page. By moving all the JavaScript statements associated with a button click into a function in the head, the button is simplified, and the body elements are much easier to identify and visualize. The functions that you wrote were of a very simple format — they did not take any inputs (instead, they accessed values directly from text or number boxes) nor did they return a value (instead, they displayed their result in the page). The more general form of a user-defined function is as follows:

    function FUNCTION_NAME(PARAMETER1, PARAMETER2, ...) {
        STATEMENTS_TO_PERFORM_THE_DESIRED_COMPUTATION

        return OUTPUT_VALUE;
    }

• Parameters are optional variables (separated by commas) that appear in the parentheses following the function name. They correspond to the function's inputs, so a function that requires one input value (such as Math.sqrt) would have one parameter inside the parentheses, while a function that requires two input values (such as Math.max) would have two parameters. When the function is called, the input values specified in the call are assigned to the parameter variables, which can then be used in performing the computation. If the function has no inputs, as was the case with the simple user-defined functions in Chapter X5, then there will be no parameters listed inside the parentheses.
• A return statement is an optional statement that can appear at the end of a function definition. A return statement consists of the word return, followed by a variable or expression. When the statement is executed, the variable or expression is evaluated, and the resulting value is returned as the output of this function.

For example, consider the following simple function definition:

    function InchesToCentimeters(inches) {
        cm = inches * 2.54;
        return cm;
    }

This function has one parameter, inches, that appears inside the parentheses. When the function is called, a number must be specified as the input to the function. For example,

    InchesToCentimeters(10)

The input specified in the function call is automatically assigned to the parameter variable when the function is called. In this case, the input value 10 is assigned to inches. The first statement in the function then uses that variable to calculate the corresponding distance in centimeters (10 * 2.54 = 25.4) and assign it to the variable cm. Finally, the return statement returns that value. If the function is called again, with a different input value, the same sequence occurs. For example, the call InchesToCentimeters(20) would result in the parameter variable being assigned 20 and the function returning 50.8.

The HTML document in EXAMPLE 7.1 contains two function definitions in the script element. The first is the InchesToCentimeters function from above; the second is the parameterless ShowInToCm function that is called when the button is clicked. The ShowInToCm function accesses the number from the box and calls the InchesToCentimeters function to perform the conversion. Both values are then displayed in the page.

        10        39.4        100        200

As you saw in previous chapters, a Web page can contain more than one button. Typically, each button will have its own function to define the action taken when that button is clicked. Similarly, if the buttons are performing complex computations, we might need multiple functions for those tasks. EXAMPLE 7.2 shows an extension to the HTML document in EXAMPLE 7.1. In addition to a button that converts inches to centimeters, there is a button that converts feet to meters. As a result, there are four functions defined: two functions defining the button actions (ShowIntoCm and ShowFttoM), with each of those functions calling another function perform a conversion (InchesToCentimeters and FeetToMeters).

It is interesting to note that the FeetToMeters function calls the InchesToCentimeters function as part of its calculation. FeetToMeters first converts from feet to inches (1 foot = 12 inches), then calls the InchesToCentimeters function to convert inches to centimeters and finally converts from centimeters to meters (100 centimeters = 1 meter). It is also worth noting that both functions access the same number box but interpret the contents as different units.

        10        50        100        5280

    Example: Random Numbers Revisited

When a calculation is needed more than once, a general-purpose function can remove redundancy and simplify the code. Consider the Pick-4 page from Chapter X6 (EXAMPLE 6.7). Since four different balls needed to be drawn, there were four statements that contained the same expression:

    pick1 = Math.floor(numBalls*Math.random() + 1);
    pick2 = Math.floor(numBalls*Math.random() + 1);
    pick3 = Math.floor(numBalls*Math.random() + 1);
    pick4 = Math.floor(numBalls*Math.random() + 1);

Devising the correct expression to generate a random integer in the range 1..numBalls was not a trivial task. It required mathematical reasoning and thorough testing to ensure that the expression worked perfectly. Once verified, the expression is still difficult to understand and modify. For example, suppose we learned that lottery balls were numbered starting at 0. We would need to modify the expression to generate random integers from the range 0..(numBalls-1). Determining how to modify it appropriately is almost as much work as devising the original formula! A better alternative is to invest the effort to create a general-purpose function, which could be used to generate a random integer from any specified range. The following function does that:

    function RandomInt(low, high) {
        return Math.floor(Math.random()*(high-low+1)) + low; 
    }

This function takes two inputs, the low and high integers from the desired range. It then uses those inputs as part of a generalized expression that generates a random integer in the range low..high. For example,

    RandomInt(1, 42)		returns a random integer from the range 1..42

    RandomInt(0, 41)		returns a random integer from the range 0..41

    RandomInt(200, 250)		returns a random integer from the range 200..250

The Web page in EXAMPLE 7.3 reimplements the Pick-4 page using the above RandomInt function. The function definition is added within the script tags in the head of the page, above the Lottery function. The inclusion of the RandomInt function in the page allows for the statements in the Lottery function to be simplified. Instead of repeating the complex expression for generating the random picks, each pick can be generated by a call to the RandomInt function.

Functions simplify the programmer's task in two important ways. First, functions help minimize the amount of detail that a programmer must keep track of. Because the Math.sqrt function is available, the programmer does not need to know the sequence of steps involved in computing a square root. Instead, they only need to know how to call the Math.sqrt function. In the Pick-4 example, defining and debugging the RandomInt function once means that it can be used in this and other pages without having to remember the logic behind it. Second, functions help minimize the length and complexity of code. Because the Math.sqrt function is available, the square root of a value can be obtained via a single call to this function. This significantly reduces code complexity because the number of steps otherwise required to compute the square root would be considerable. Likewise, the modified Pick-4 page from EXAMPLE 7.3 is easier to understand because the messy details are moved to the RandomInt function.

      More General-purpose Functions

Whenever a complex computation is required, especially a computation that may be repeated in a page or across multiple pages, it is worthwhile to encapsulate that computation in the form of a function. Three additional examples of general-purpose functions are provided in FIGURE 1.

  function Greeting(firstName, lastName) {
      return 'Hello ' + firstName + ' ' + lastName +   
             '. May I call you ' + firstName + '?';
    }

  function Distance(x1, y1, x2, y2) {
      term1 = (x1-x2)**2;
      term2 = (y1-y2)**2;

      return Math.sqrt(term1 + term2);
    }

  function CompoundInterest(amount, rate, years) {
      return amount * (1+rate/10)**years;
  }

1. The Greeting function in FIGURE 1 demonstrates that functions are not limited performing mathematical computations only. This function takes two inputs, string values representing a person's first and last names, and returns a message using those inputs. For example,

       Greeting('Chris', 'Jones')	       returns the string 'Hello Chris Jones. May I call you Chris?'
   
       Greeting('Pat', 'Martinez')	       returns the string 'Hello Pat Martinez. May I call you Pat?'

2. The Distance function in FIGURE 1 calculates the distance between two points: (x1, y1) and (x2, y2). This function takes four inputs, numbers representing the x and y coordinates of the two points. It breaks this complex formula into individual steps, first calculating the values (x1-x2)² and (y1-y2)², assigning those values to variables, and then combining them for the final return value. For example,

       Distance(10, 0, 10, 6)             returns 6    
   
       Distance(0, 0, 3, 4)               returns 5    
   

3. The CompoundInterest function in FIGURE 1 calculates the compound interest accrued over a period of years given an initial amount and interest rate. This function takes three inputs, numbers representing the initial investment amount, the annual interest rate, and the number of years. It calculates and returns the total amount accumulated over those years. For example,

       CompoundInterest(50, 10, 1)        returns 55    	
   
       CompoundInterest(100.0, 4, 18)     returns 202.58   
   

    Example: Distance Revisited

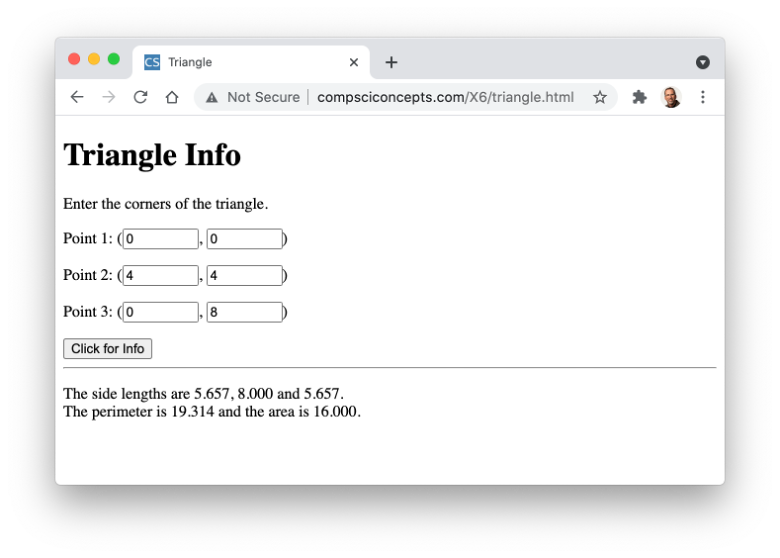
The Distance page from Chapter X6 (EXAMPLE 6.6) enabled you to enter the x and y coordinates of two points into number boxes. At the click of a button, the distance between those two points was calculated and displayed in the page. The HTML document in EXAMPLE 7.4 generalizes this page to now include coordinates for three points, the corners of a triangle. The Distance function from FIGURE 1 above is defined in the page and subsequently called three times in the ShowInfo function to calculate the lengths of each triangle side. The side lengths are then summed to calculate the triangle's perimeter.

Similar to Pick-4 (EXAMPLE 7.3), this example demonstrates the power of functions. The definition of the Distance function contains all the messy details involved in calculating the distance between two points. Once that function is defined in the page, it can be called repeatedly. The ShowInfo function is shorter and simpler than it would have been if the distance calculations had been duplicated three times. Since the name of the Distance function reasonably describes its purpose, the calls to that function are easily understood even if the details of how the function works are not.

      Libraries of Functions

If a complex calculation is required in a page, defining a general-purpose function to abstract away the details of that calculation has multiple advantages. It simplifies the page by moving the details of the calculation into the head. If multiple instances of that computation are required within the page (as in the Pick-4 and Triangle pages), defining the function once and then calling it multiple times can shorten the code considerably. Plus, if an error is later discovered or a modification to the calculation is required, the changes need only be made to the function definition as opposed to throughout the page.

If a function or collection of functions is especially useful, it might be included in many pages. For example, the RandomInt function could prove useful in a variety of applications. It would become tedious to copy-and-paste the function definition into every page that needs it. Even worse, duplication of the same function definition in multiple locations can lead to major maintenance issues. To fix an error or make a modification, you would need to locate every page that contains that definition and update them all.

Fortunately, there is a better way to manage functions that are to be shared across multiple pages. Useful functions can be placed in a separate text file known as a library file. That library file of functions can then be loaded into any Web page using a script element with a src attribute specifying the file name:

    <script src="LIBRARY_FILE_NAME"></script> 

When placed in the head of a Web page, this script element has the effect of loading those function definitions from the specified file, which can then be called within the page (the same as if they were entered directly into the page). Note that nothing appears between the script tags. You can think of the src attribute as directing the browser to retrieve the functions from the specified library file and insert them between the script tags. If you did place anything in between the script tags, it would be overwritten when the library contents are loaded.

    The random.js Library

The RandomInt function, along with three other useful functions involving randomness, are defined in a library file named random.js (which is accessible online at https://freecsc.com/random.js). Descriptions of the four functions in this library file are provided in FIGURE 2.

Any page can load the random.js library by including the following script element in the head.

    <script src="https://freecsc.com/random.js"></script> 

This element loads the contents of the library file into the page, making the definitions of the functions RandomInt, RandomNum, RandomChar and RandomOneOf accessible within that page. Utilizing a library file is the ultimate application of abstraction. The page developer can use the functions from a library file without even looking at their definitions!

The HTML document in EXAMPLE 7.5 reimplements the Pick-4 page (EXAMPLE 7.3) using the random.js library. The script element in the head loads the random.js library file into the page, making the functions from that file (including RandomInt) accessible within the page. The RandomInt function is then called to generate the random picks as before. Note that details of the RandomInt function are completely hidden, making this final version of the Pick-4 page the most succinct and clear.

    Example: Dice Simulations

The HTML documents in EXAMPLES 7.6 and 7.7 further demonstrate the utility of the random.js library. Both documents utilize functions from the library to perform the same task — simulating the roll of two dice and displaying that roll as die images. Note that image files for each of the six die faces are stored in the book's Images directory using the names die1.gif, die2.gif, ..., die6.gif.

In EXAMPLE 7.6, the RandomInt function is called to generate random integers in the range 1 to 6. Those random integers are then used to construct the Web addresses of the die images. For example, if the variable roll1 is assigned the random integer 4, then:

	die1Img.src = 'https://freecsc.com/Images/die' + roll1 + '.gif';
		          ⇊ 
	              'https://freecsc.com/Images/die' + 4 + '.gif';
		          ⇊ 
	              'https://freecsc.com/Images/die4.gif';

In EXAMPLE 7.7, the RandomOneOf function is called to select a random file name from a list of options. The file name is then used to construct the Web addresses of the die images. For example, if the variable roll1 is assigned the random string 'die6.gif,' then:

	die1Img.src = 'https://freecsc.com/Images/die' + roll1;
		          ⇊ 
                      'https://freecsc.com/Images/' + 'die6.gif';
		          ⇊ 
                      'https://freecsc.com/Images/die6.gif';

    RandomOneOf(['yes', 'no', 'maybe'])	

    RandomOneOf('yes', 'no', 'maybe') 

    Example: Random Sequence Generation

Many secure computer systems require the use of complex passwords that are difficult to guess. One way to create secure passwords is to automatically generate them as random sequences of characters. While a hacker might be able to guess your password if it is the name of your family dog or your fifth-grade teacher, it is extremely unlikely that they would be able to guess a random password such as d6CW4!m.

Recall that the RandomChar function from the random.js library takes a string as input and returns a randomly selected character from that string. The HTML document in EXAMPLE 7.8 utilizes this function to generate random character sequences, which could be used for password creation. The page contains a text box in which the user enters the characters to choose from. By default, this box contains the entire alphabet, but the user can enter any sequence of characters they desire (e.g., '0123456789' to generate random numbers). When the button is clicked, the contents of the text box is accessed and the RandomChar function is called to select random characters from the box contents. Three random characters are chosen, glued together, and displayed in the page.

      Putting It All Together

Although there is no scientific evidence that Extrasensory Perception (ESP) exists, some people claim to have the ability to predict the future. We can create a Web page that will allow you to test your supposed ESP powers. The page will allow you to guess a number from 1 to 3 and then will match your guess against a randomly generated number in that range. If you are correct more than a third of the time, which is what you would expect from random guesses, then you might claim to have some level of ESP. Or, realistically, you were just lucky and subsequent unlucky guesses would eventually balance things out. For example:

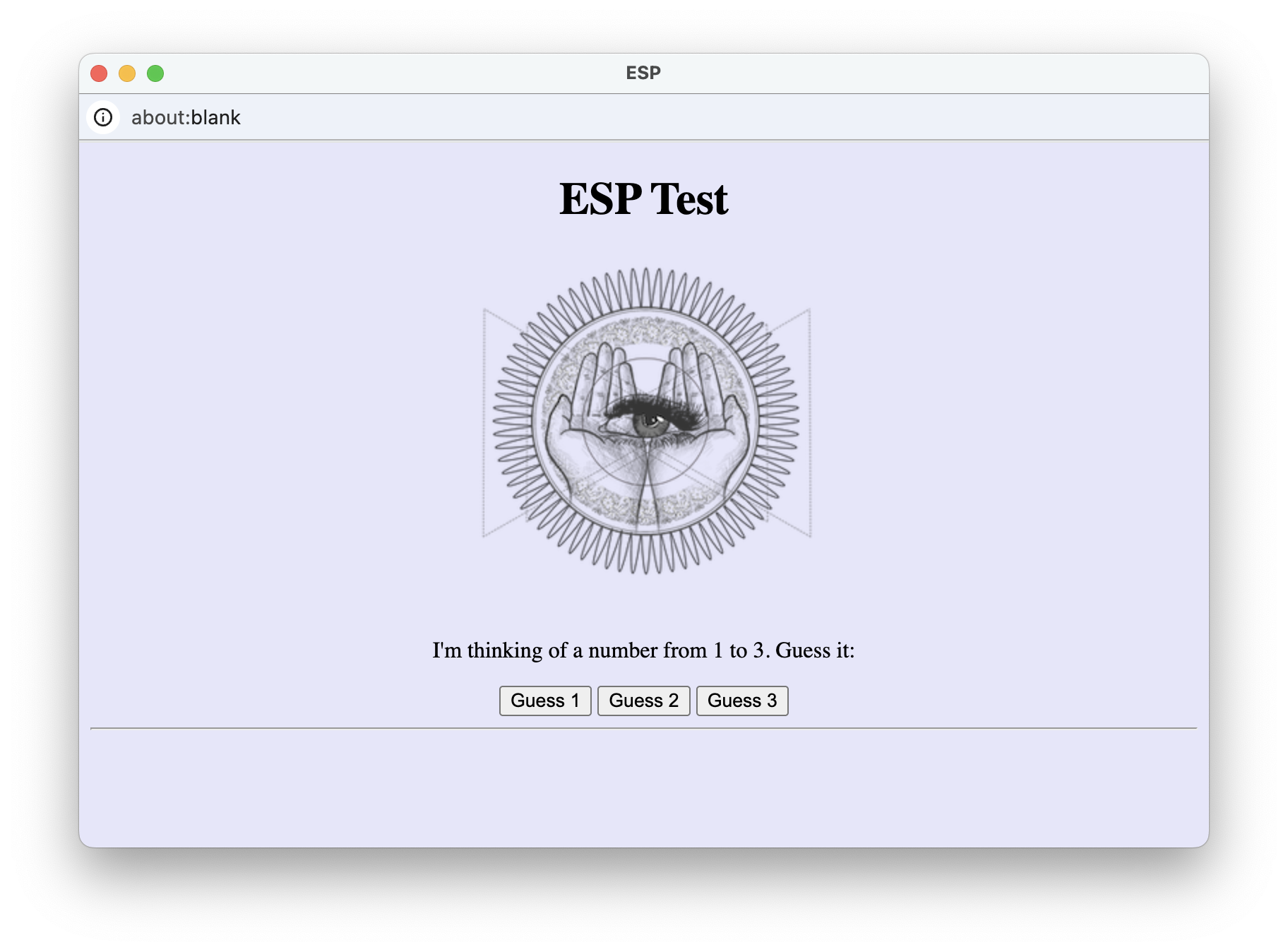
The HTML document in EXAMPLE 7.9 takes a first pass at implementing this page.

There are several details to note about this document and how it implements the desired appearance and behavior of the page.

• Since there are three possible guesses, there are three button elements with corresponding functions. For example, clicking on the "Guess 1" button will call the Guess1 function that displays the computer's random number and the user's guess of 1. Similarly, the "Guess 2" button calls the Guess2 function and the "Guess 3" button calls the Guess3 function.
• Within the functions, the RandomInt function from the random.js library is used to pick the computer's number. The library is loaded by a dedicated script element in the head section, with attribute src="https://freecsc.com/random.js".
• A style attribute in the <body> tag is used to center the page contents and set the background color to lavender. Similarly, a span element is used in the messages so that the numbers are purple and double-sized.

In general, redundancy is something to avoid when developing an interactive Web page. Not only does it make the code longer and more difficult to read, but it also makes it harder to debug and/or modify. For example, if we decided that we wanted to change the message displayed in the ESP page, e.g., displaying the numbers in pink instead of purple, we would have to make identical modifications in all three functions.

Fortunately, parameters provide a way of avoiding such redundancy. Instead of three functions, identical except for the user's guess, we could have a single function with a parameter. When called, the user's guess would be specified as the input and then would be assigned to the parameter within the single function. EXAMPLE 7.10 makes this modification. Note that there is only one function, named Guess, which has a parameter named guess. That parameter variable is then used in the message to display the guess. For example, if the "Guess 1" button is clicked, then the call is Guess(1), which assigns 1 to the guess parameter and displays it as part of the message. Similarly, the "Guess 2" button calls Guess(2) and the "Guess 3" button calls Guess(3).

      Chapter Summary

• Abstraction is the process of ignoring minutiae and focusing on the big picture when performing a task.
• Functions simplify the programmer's task by (1) minimizing the amount of detail that the programmer must keep track of, (2) minimizing the size and complexity of code, and (3) centralizing code so that changes need only be made in one place.
• The general form of a user-defined function is as follows:

      function FUNCTION_NAME(PARAMETER1, PARAMETER2,...) {
          STATEMENTS_TO_PERFORM_THE_DESIRED_COMPUTATION 
          return OUTPUT_VALUE;  
      } 

• A parameter is a function-specific variable. When a function is called, its parameters are automatically assigned values corresponding to the input values in the call (the first input value is assigned to the first parameter variable, the second input value to the second parameter variable, ...).
• A return statement specifies the value that should be returned by the function. When a return statement is executed, the function call terminates, and the value specified in the return statement is returned as the output of that call.
• Parameters and a return statement are optional in a function definition. For example, a function that accesses data directly from text or number boxes may not require parameters. Likewise, a function that displays a message in a paragraph may not require a return statement.
• User-defined functions can be defined directly in the head of a Web page, enclosed in script tags.
• General-purpose functions that might be used in many different pages can be placed in separate library files and then loaded into Web pages as needed. To load a library file, use a script element of the form:

      <script src="LIBRARY FILENAME"></script> 

• The random.js library (accessible as https://freecsc.com/random.js) defines functions for generating a random integer in a specified range (RandomInt), a random real number in a specified range (RandomNum), a random character from a string (RandomChar), and a random item from a list (RandomOneOf).

      Projects

All projects should follow the basic design guidelines described in this and the previous chapters. These include:

• If there is a complex calculation that needs to take place in the page, especially one that is used more than once, a user-defined function with parameters and a return statement should be added to the head section within script tags.
• If user-defined functions could reasonably be used in multiple pages, e.g., the random functions introduced in this chapter, then those functions should be defined in a library file that is linked to by the appropriate pages.

PROJECT 7.A: The ESP pages from EXAMPLES 7.9 and 7.10 provided separate buttons for each guess. As a result, expanding the numbers that can be guessed, say 1-5, will require adding more buttons. Consider an alternative approach using two number boxes. The first allows you to enter the maximum number that can be guessed; the second number box allows you to enter your guess. There is a single button in the page that submits that guess and produces a message similar to EXAMPLES 7.9 and 7.10. Note that the random pick should be between 1 and the number in the first box. For example,

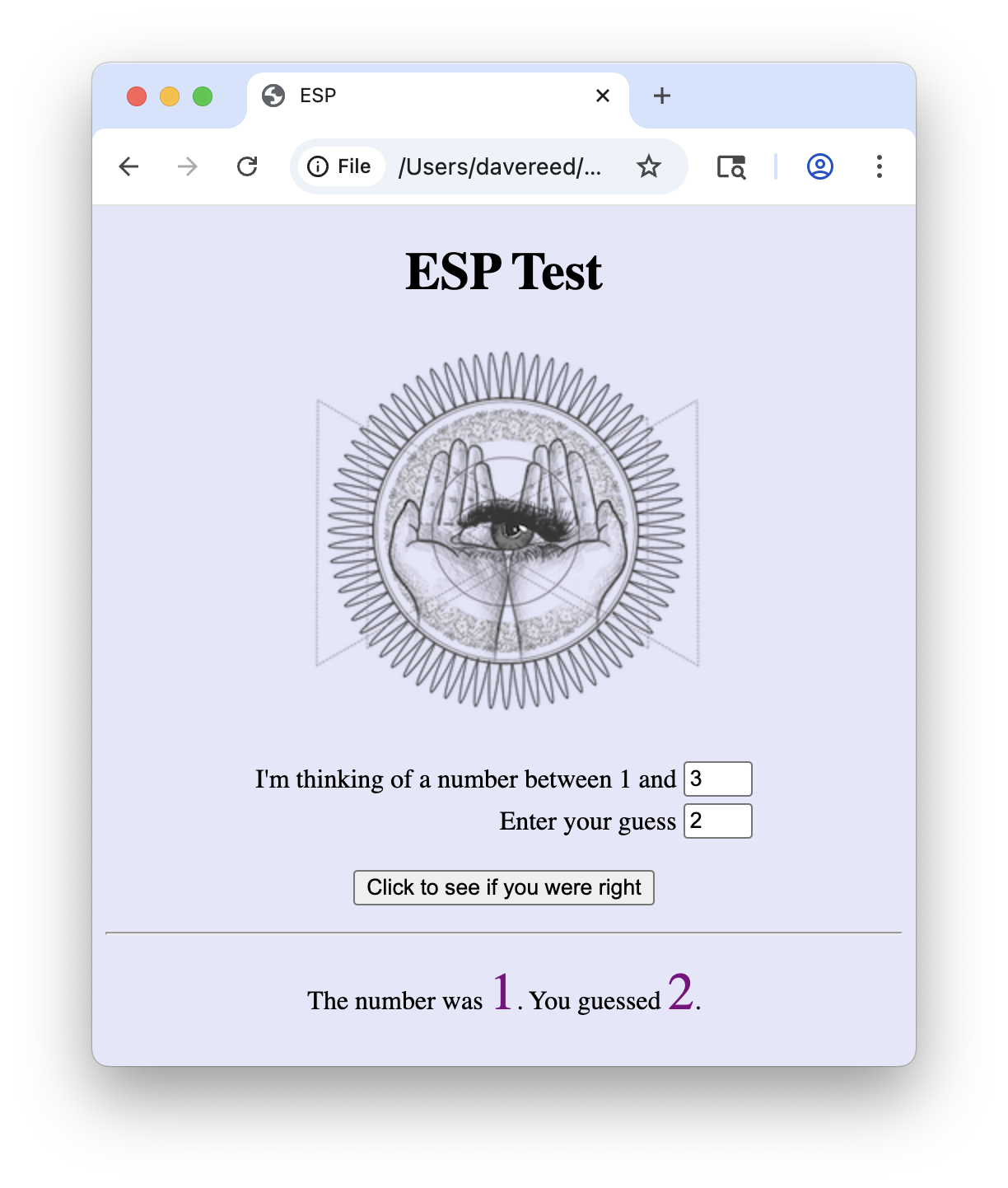
Download a copy of the HTML document in EXAMPLE 7.10 (by clicking on the Download link) and save it on your computer under the name esp.html. Using a text editor of your choice, modify the document so that it uses the two number boxes as described above.

Note: this design produces a more flexible page in that you can adjust the range of possible numbers simply by changing the number in a box. However, there is a price — if you accidentally enter a number from outside that range, there will be no error message. In EXAMPLES 7.9 and 7.10, it was impossible for you to enter an invalid number since three buttons corresponded to the three valid options.

PROJECT 7.B: Create a Web page named coin.html that contains a single coin image. When the user clicks on that image, a function in your page should randomly choose a coin face (using the RandomOneOf function from the random.js library) and display that face. There should be a caption below the coin image that initially displays 'Click on the coin to flip.' After each simulated flip, the caption should be changed to identify the flip result, either 'You flipped heads.' or 'You flipped tails.' For example, the page might initially appear as:

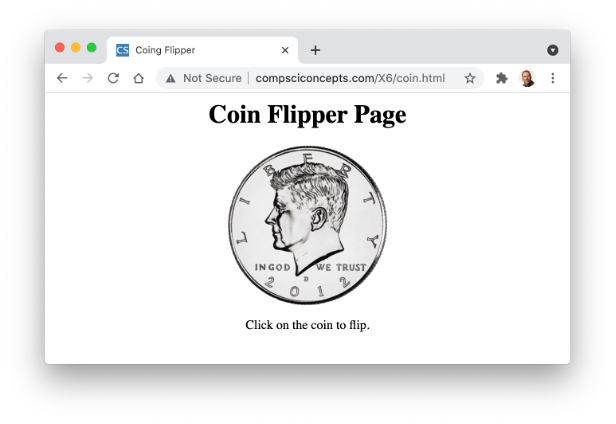
After a flip of tails, it might appear as:

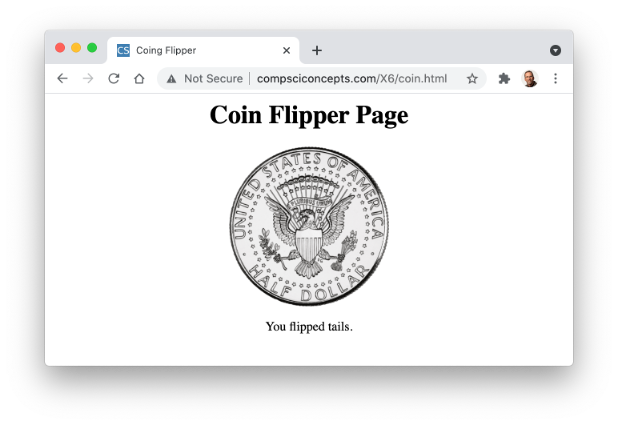
Hint: To make things simpler, locate and download coin images from the Web (there are many free options that can be found). Rename those image files heads.XXX and tails.XXX, where XXX is the existing file extension (e.g., jpg).

When you are testing your page, don't be alarmed if you click on the image and nothing changes. After all, there is a 50% chance that you will obtain the same face that is already showing (i.e., it is showing HEADS and flips HEADS). Use your modified page to simulate repeated coin flips. Did you obtain roughly 50% heads and 50% tails?

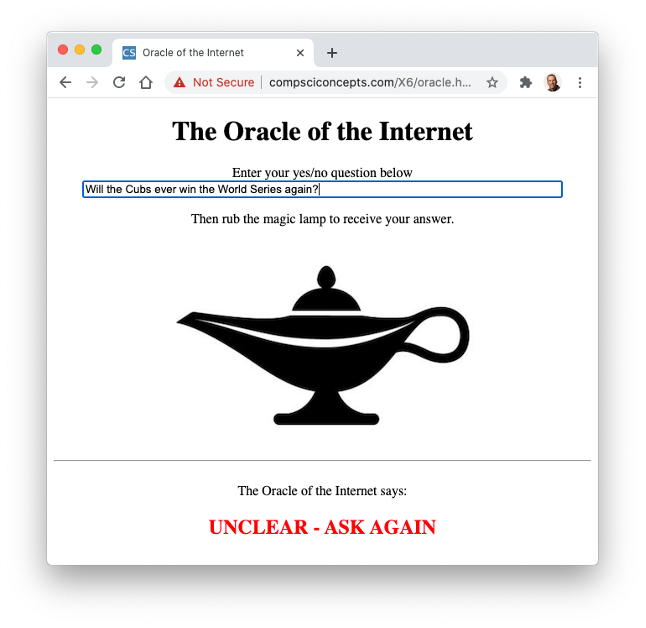
PROJECT 7.C: In ancient Greece, the Oracle of Delphi was a priestess widely believed to be able to prophesize the future. People would travel from across the Hellenistic world to the temple at Delphi to consult with the Oracle on personal or professional matters. Using the RandomOneOf function from the random.js library, it is possible to select from a list of predetermined responses and so create a page that acts as a modern-day oracle.

Create a Web page named oracle.html that simulates the functionality of an oracle by answering yes/no questions posed by the user. Your page should look like the one below, with a text box for entering a question and some interactive image (the choice of image is up to you). When the mouse moves over the image, a function should be called to select a random response from a list of at least five possible responses and display the response in a page division. When the mouse moves off, the answer should disappear. The oracle's answer should be in a large, red font. For example,

PROJECT 7.D: Heron's formula can be used to calculate the area of a triangle given the lengths of its sides (s1, s2 and s3):

    area = √p(p-s1)(p-s2)(p-s3)     where p=(s1+s2+s3)/2

Download a copy of the Triangle page from EXAMPLE 7.4 and save it under the name triangle.html. from the book's code directory and store it on your computer under the same name.

1. Create a library file named geometry.js on your computer (in the same directory as your triangle.html page). Cut-and-paste the definition of the Distance function into this library file. In addition, add a function named TriangleArea that calculates the area of a triangle using Heron's formula. The function should take three inputs, representing the lengths of the three triangle sides. For example, the call TriangleArea(3,4,5) should return 6.
2. Modify your triangle.html page so that it utilizes the functions from your geometry.js library file to calculate and display the side lengths, perimeter, and area of the triangle. All the numbers should be rounded to 3 decimal places when displayed. For example,