C8: Inside Data
Digital is to analog as steps are to ramps. — Anonymous
You can have data without information, but you cannot have information without data. — Daniel Keys Moran
In Chapter C1, we defined a computer as a device that receives, stores, and processes data. This chapter returns to the concepts of data and storage, detailing how data is represented inside a computer. Modern computers store data as digital signals (i.e., sequences of 0s and 1s), but the technology used to retain these signals varies greatly, depending on the storage device and type of data. For example, RAM memory stores data as electrical currents in circuitry, whereas CD-ROMs store data as sequences of pits burned into the disk. However, despite differences among storage technologies, most employ the same sets of rules for converting data into 1s and 0s. For example, nearly all programs use the same coding standard for specifying text characters as 8-bit patterns. Similar conventions exist for representing other data types, including numbers and images.
This chapter describes common formats and standards that computers use to represent data. After covering the basics of digital representation, we explain how specific data types such as integers, real numbers, and text are stored on computers. Because most data representations involve binary numbers, a review of binary-number systems is also provided.
Analog vs. Digital
Data can be stored electronically in two ways, either as analog or digital values. Analog values represent data in a way that is analogous to real life, in that such values can vary across an infinite range of values. By contrast, digital values utilize only a discrete (finite) set of values. For example, temperature is inherently analog, with degrees that can range continuously. For a scientific experiment, the difference between 110.36804 and 110.36805 degrees Fahrenheit might be significant. Analog thermometers measure temperature on a continuous scale, often using a column of heat-sensitive liquid that expands along a scale. By contrast, digital thermometers represent temperatures as discrete values, often rounded to tenths of degrees. When measuring a person's temperature, anything beyond that level of precision is unnecessary and so a simple digital display suffices (FIGURE 1, top left).
Many other types of data can be represented alternatively as analog or digital values, depending on the device or technology involved. An analog clock measures time by the position of hands that move continuously around a circle, whereas a digital clock displays time as discrete units: hours, minutes and seconds (FIGURE 1, top-right). An analog radio displays station broadcast frequencies as continuous positions on a dial, with knobs that allow the use to select and fine tune the reception. Digital radios utilize discrete numbers (with AM stations measured in increments of 10 kilohertz and FM stations measured in increments of 0.1 megahertz) and often utilize buttons to move up or down one increment (FIGURE 1, bottom-left). In many settings, it is common to see both analog and digital data side-by-side. The bottom-right of FIGURE 1 shows an analog speedometer, which represents a car's speed as a needle on a continuous arc, directly above a digital odometer, which shows the car's mileage as a sequence of discrete digits.

FIGURE 1. Analog vs. digital thermometers (Polina Tankilevitch/Pexels), watches (Ball Watch Co./Wikimedia Commons, Petar Milosevic/Wikimedia Commons), car stereos and gauges (Havard Wien/Wikimedia Commons, Sav127/Wikimedia Commons).
 Grammatically Speaking
Grammatically Speaking
It is interesting to note that the distinction between analog (continuous) values and digital (discrete) values has grammatical significance. Continuous values are compared using less while discrete values are compared using fewer. For example, we might say Pat has less money than Chris, but fewer dollars, since money is continuous, and dollars are discrete. Similarly, Wire1 has less current flowing through it than Wire2, but carries fewer volts. Likewise, Task1 may take less time than Task2, but requires fewer minutes.
The primary trade-off between analog and digital data representation is variability versus reproducibility. Because an analog system encompasses a continuous range of values, a potentially infinite number of unique values can be represented. For example, the dial on an analog radio receiver allows you to find the exact frequency corresponding to the best possible reception for a particular station. However, this dial setting may be difficult to reproduce. If you switched to another station for a while and then wanted to return to the previous one, relocating the perfect frequency setting would involve fine-tuning the dial all over again. With a digital radio receiver, frequencies are rounded to discrete values. So, while a digital setting for a particular station such as 106.9 might not be the exact, optimal frequency, it is easy to remember and reselect.
In general, analog representations are ideal for storing data that is highly variable but does not have to be reproduced exactly. Analog radios are functional because station frequencies do not need to be precise — you can listen to a station repeatedly without selecting the precise optimal frequency every time. Likewise, analog thermometers and clocks are adequate for most purposes, as a person rarely needs to reproduce the exact temperature or time — rough estimates based on looking at the devices usually suffice. However, the disadvantages of analog representation can cause problems under certain circumstances. For example, audio cassettes store music in an analog format, representing the continuous sound waves as magnetic signals on a tape. Copying a cassette introduces errors as the continuous values are reproduced, and copying a copy introduces even more errors, degrading the sound quality.
When it comes to storing data on a computer, reproducibility is paramount. If even a single bit is changed in a file, the meaning of the data can be drastically altered. Thus, modern computers are digital devices that save and manipulate data as discrete values. The specific means of storage depends on the technology used. For example, an electrical wire might carry voltage or no voltage, a switch might be open or closed, a capacitor might be charged or not charged, a location on a hard drive might be magnetized or not magnetized, and a location on a CD might be reflective or nonreflective. What all these technologies have in common is that they distinguish between only two possibilities. To simplify discussion, the two (binary) states stored by digital devices are typically referred to as 0 and 1. Thus, a voltage-carrying wire or a magnetized spot on a floppy disk can be thought of as a 1, whereas a wire with no voltage or a non-magnetized spot can be thought of as a 0. Because these 1s and 0s — called binary digits, or bits — are central to computer data representation, the next section provides an overview of binary number systems.
✔ QUICK-CHECK 8.1: True or False? In contrast to digital signals, analog signals use only a discrete (finite) set of values for storing data.
✔ QUICK-CHECK 8.2: In addition to the examples given in this chapter, identify a real-world device that can use either an analog or digital representation of data.
Binary Number System
As humans, we are used to thinking of numbers in their decimal (base 10) form, where individual digits correspond to escalating powers of ten. When dealing with decimal numbers, the rightmost digit is the 1s place (100 = 1), the next digit is the 10s place (101 = 10), the next is the 100s place (102 = 100), and so on. Our use of the decimal number system can be seen as a natural result of evolution, since humans first learned to count on ten fingers. Evolutionary bias aside, however, numbers can be represented using any base, including binary (base 2). In the binary number system, all values are represented using only the two binary digits (bits), 0 and 1. As with decimal numbers, different bits in a binary number correspond to different powers — however, the bits specify ascending powers of 2 instead of 10. This means that the rightmost bit is the 1s place (20 = 1), the next bit is the 2s place (21 = 2), the next the 4s place (22 = 4), and so on. To distinguish binary numbers from their decimal counterparts, we can add a subscript identifying the base. For example, 11012 would represent the binary number that is equivalent to 13 in decimal (FIGURE 2).
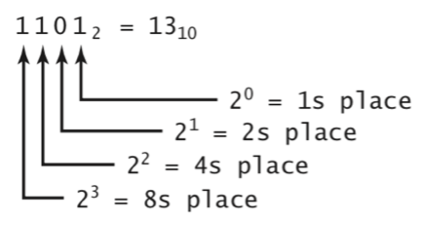
FIGURE 2. Bit positions in a binary number.
In general, converting a binary number to its decimal equivalent is straightforward: simply multiply each bit (either 1 or 0) by its corresponding power of two and sum the results. FIGURE 3 shows the steps in converting 11012 into its decimal equivalent, 13. You can change the bits in the box and click the button to perform other conversions.
FIGURE 3. Interactive Decimal to Binary converter.
✔ QUICK-CHECK 8.3: Using the interactive converter in FIGURE 2, determine the decimal equivalents of the following binary numbers: 1012, 1112, 11102, 1000002, 1000012.
When using the converter in FIGURE 2, you may have noticed that binary numbers that end in 1 are always odd, whereas binary numbers that end in 0 are even. This makes sense when you recognize that the decimal value of a binary number is a sum of powers of two (corresponding to the places of the bits). Since 20 is the only odd power of two, it must be included in an odd sum, meaning the rightmost bit of an odd number must be a 1.
Another interesting property of binary numbers is that adding a 0 bit to the end of a number doubles its value. For example, 112 represents the decimal value 3, 1102 represents 6, 11002 represents 12, and so on. When you add a 0 bit at the end, all the other bits shift one place to the left. Thus, the bit from the 1s position is now in the 2s position, the bit from the 2s position is now in the 4s position, and so on. The position of each shifted bit doubles, and so does the sum.
FIGURE 4 shows the opposite conversion, from decimal to binary. Essentially, the number is factored into powers of 2, which then correspond to individual bits. As before, you can change the decimal number in the box and click the button to perform other conversions.
FIGURE 4. Interactive Binary to Decimal converter.
✔ QUICK-CHECK 8.4: Using the interactive converter in FIGURE 3, determine the binary equivalents of the following decimal numbers: 6, 16, 17, 66, 75.
✔ QUICK-CHECK 8.5: If a binary number ends in a 0, it follows that removing that bit at the end yields a binary number whose value is half the original.
Representing Numbers
Since computers retain all information as bits (0 or 1), binary numbers provide a natural means of storing integer values. When an integer value must be saved in a computer, its binary equivalent can be encoded as a bit pattern and stored using the appropriate digital technology. Thus, the integer 19 can be stored as the bit pattern 10011, whereas 116 can be stored as 1110100. However, because binary numbers contain varying numbers of bits, it can be difficult for a computer to determine where one value in memory ends and another begins. Most computers and software avoid this problem by employing fixed-width integers. That is, each integer is represented using the same number of bits (usually 32 bits). Leading 0s are placed in front of each binary number to fill the 32 bits. Thus, a computer would represent 19 as:
00000000000000000000000000010011
Given that each integer is 32 bits long, 232 = 4,294,967,296 different bit patterns can be represented. By convention, the patterns are divided as evenly as possible between positive and negative integers. Thus, programs that use 32-bit integers can store 232/2 = 231 = 2,147,483,648 non-negative numbers (including 0) and 232/2 = 231 = 2,147,483,648 negative numbers. The mapping between integers and bit patterns is summarized in FIGURE 5.

FIGURE 5. Representing integers as bit patterns.
While examining the integer representations in FIGURE 4, you may have noticed that the bit patterns starting with a 1 correspond to negative values, while those starting with a 0 correspond to non-negative values. Thus, the initial bit in each pattern acts as the sign bit for the integer. When the sign bit is 0, then the remaining bits are consistent with the binary representation of that integer. For example, the bit pattern corresponding to 3 begins with 0 (the sign bit) and ends with the 31-bit binary representation of 3: 0000000000000000000000000000011. Similarly, the bit pattern corresponding to 100 consists of a 0 (the sign bit) followed by the 31-bit representation of 100: 0000000000000000000000001100100.
Surprisingly, the negative integers do not follow this same pattern. In fact, the negative numbers are reversed so that the negative integer with the largest absolute value (2-31) corresponds to the smallest bit pattern (10000000000000000000000000000000), whereas the negative integer with the smallest absolute value (-1) corresponds to the largest bit pattern (111111111111111111111111111111111). This notation, known as two's-complement, has several advantages over the simplistic approach of just adding a 1 at the front to make a number negative. First it avoids having two zero values (0 and -0), which can be confusing. Second, for technical reasons beyond the scope of this text, it makes adding positive and negative numbers much simpler.
✔ QUICK-CHECK 8.6: Using 32 bits, the largest integer value that can be represented is 231 - 1, whereas the smallest negative value is -231. Why aren't these ranges symmetric? That is, why is there one more negative integer than there are positive integers?
Real Numbers
Because digital computers store all data as binary values, the correlation between integers and their binary counterparts is relatively intuitive. Real values can also be stored in binary, but the mapping is not quite so direct. The standard approach utilizes scientific notation to normalize real numbers into a standard format. For example, the number 1234.5 can be equivalently represented in scientific notation as 0.12345 x 104. In a similar way, any real number can be normalized so that all the digits are to the right of the decimal place, with the exponent adjusted accordingly:
| 1234.5 → 0.12345 X 104 | 0.0099 → 0.99 X 10--2 | |
| -510.0 → -0.51 X 103 | 0.00000001 → 0.1 X 10-7 |
Any real number can be uniquely identified by the two components of its normalized form: the fractional part (the digits to the right of the decimal place) and the exponent (the power of 10). For example, the real value 1234.5, which normalizes to 0.12345 x 104, could be represented by the integer pair (12345, 4). Similarly,
| 1234.5 → 0.12345 X 104 → (12345, 4) | 0.0099 → 0.99 X 10--2 → (99, -2) | |
| -510.0 → -0.51 X 103 → (-51, 3) | 0.00000001 → 0.1 X 10-7 → (1, -7) |
Real numbers stored in this format are known as floating-point numbers, since the normalization process shifts (or floats) the decimal point until all the digits are to the right of the decimal place, adjusting the exponent accordingly. In 1985, the Institute of Electrical and Electronics Engineers (IEEE) established a standard format for storing floating-point values that has since been adopted by virtually all computer and software manufacturers. According to the IEEE standard, a floating-point value can be represented using either 32 bits (4 bytes) or 64 bits (8 bytes). The 32-bit representation, known as single precision, allots 24 bits to store the fractional part (including the sign bit) and 8 bits to store the exponent, producing a range of potential positive values that spans from approximately 1.2 x 10-38 to 3.4 x 1038 (with an equivalent range for negative numbers). By contrast, the 64-bit representation, known as double precision, allots 53 bits for the fractional part (including the sign bit) and 11 bits for the exponent, yielding a much larger range of potential positive values (from approximately 2.2 x 10-308 to 1.8 x 10308). See FIGURE 6 for a visualization.
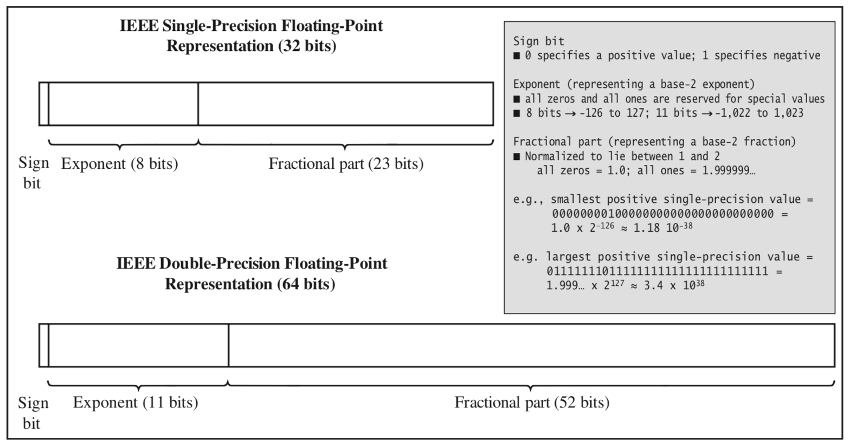
FIGURE 6. IEEE floating-point representations.
Many details of the IEEE single-precision and double-precision formats are beyond the scope of this text. For our purposes, what is important is to recognize that a real value can be converted into a pair of integer values (a fraction and an exponent) that are combined to form a representative binary pattern. It is interesting to note that certain bit patterns are reserved for special values, such as the NaN (Not a Number) utilized by JavaScript. Any bit pattern in which the exponent bits are all 1s and the fractional part is non-zero is interpreted as NaN.
As there are an infinite number of real values and only a finite number of 32- or 64-bit patterns, it is not surprising that computers are incapable of representing all real values, even among those that fall within the attainable range. When the result of a calculation yields a real value that cannot be represented exactly, the computer will round off the value to the pattern with the closest corresponding value. In a single-precision floating-point number, roughly 7 decimal digits of precision are obtainable. That is, the computer will round off any real value containing more than 7 significant digits. Using double precision, approximately 16 decimal digits of precision are obtainable. The fact that JavaScript uses double precision to represent numbers explains why 0.9999999999999999 (with 16 9s to the right of the decimal) is represented exactly, whereas 0.99999999999999999 (with 17 9s) is rounded up to the value 1.
Most programming languages differentiate between integer and real values, using 32-bit patterns for storing integers and a floating-point format for storing real numbers. However, JavaScript simplifies number representation by providing only a single number type, which encompasses both integers and reals. Thus, all numbers in JavaScript are stored using the IEEE's double-precision floating-point format.
✔ QUICK-CHECK 8.7: TRUE or FALSE? The following expressions represent the same number:
32.5 325 x 10-1 3.25 x 101 0.325 x 102
✔ QUICK-CHECK 8.8: TRUE or FALSE? As the IEEE double-precision format uses more bits than the single-precision format does, it allows for a wider range of real values to be represented.
Representing Text
Unlike integers and real values, characters have no natural correspondence to binary numbers. Thus, computer scientists were required to devise arbitrary systems for representing characters as bit patterns. The standard code for representing characters, known as ASCII (American Standard Code for Information Interchange), maps each character to a specific 8-bit pattern. The ASCII codes for the most common characters are listed in FIGURE 7.

FIGURE 7. The ASCII character set.
Note that digits, uppercase letters, and lowercase letters are each represented using consecutive binary numbers: digits are assigned the binary numbers with decimal values 48 through 57, uppercase letters are assigned values 65 through 90, and lowercase letters are assigned values 97 through 122. These orderings are important because they enable software to easily perform comparisons of character values. For example, the JavaScript expression ('a' < 'b') evaluates to true, because the ASCII code for the character 'a' is smaller than the ASCII code for 'b'. It is also clear from this system that uppercase letters have lower values than lowercase letters do. Thus, the JavaScript expression ('A' < 'a') evaluates to true.
The ASCII code was devised in the early 1960s when the English language dominated the scientific and computing communities. At that time, having an 8-bit code was sufficient since 256 characters were enough to represent the letters, digits and symbols that might appear in a document. As the scientific and computing communities grew in size and diversity, it became clear that an 8-bit, English-centric code could not equitably serve the global community. The Chinese language, for example, encompasses thousands of characters and it would be impossible to differentiate between all of them using one byte of memory. In 1987, the 8-bit ASCII code was extended to the 16-bit Unicode. With 16 bits, Unicode can represent 216 = 65,536 different characters, making it capable of supporting most languages. To simplify the transition to Unicode, the designers of the new system made it backward compatible with ASCII; this means that the Unicode for an English-language character is equivalent to its ASCII code, preceded by eight leading 0s. Thus, 'f' is 01100110 in ASCII and 0000000001100110 in Unicode.
✔ QUICK-CHECK 8.9: As Unicode uses twice the number of bits to represent a character than ASCII (16 vs. 8), it can represent twice as many characters.
Strings
ASCII and Unicode define how a single character can be represented by an 8- or 16-bit number. As strings are just sequences of characters, a string can be represented as a sequence of ASCII or Unicode numbers corresponding to those characters. For example, the string 'foobar' is specified in ASCII using the bit pattern listed in FIGURE 8. The first byte (8 bits) in this pattern is the ASCII code for 'f', the second byte is the code for 'o', and so on.

FIGURE 8. Representing a string as a sequence of ASCII codes.
Since ASCII and Unicode codes are all the same length (8 and 16 bits per character, respectively), storing and subsequently extracting the characters from text is straightforward. For example, a plain ASCII text file containing 100 characters would be stored as 100 bytes, with each byte representing a character. A program that wanted to process or display the file contents could access the file one byte at a time, converting each byte into its corresponding character. Similarly, a Unicode text file would require 200 bytes to represent the 100 characters.
✔ QUICK-CHECK 8.10: Assuming that a string is stored as a sequence of ASCII codes corresponding to individual characters, how would the string "CU#1" be represented?
✔ QUICK-CHECK 8.11: TRUE or FALSE? Storing an essay in a Unicode text file will require twice the memory space as storing that same essay in an ASCII text file.
How Computers Distinguish among Data Types
In this chapter, you have seen that numbers and text are stored on a computer as sequences of bits. The obvious question you may be asking yourself at this point is: How does the computer know what type of value is stored in a particular piece of memory? If the bit pattern 01100001 is encountered, how can the computer determine whether it represents the integer 97, the exponent of a real number, or the character 'a'? The answer is that, without some context, it can't! If a program stores a piece of data in memory, it is up to that program to remember what type of data that bit pattern represents. For example, suppose you wrote JavaScript code that assigned the character 'a' to a variable. In addition to storing the corresponding bit pattern (01100001) in memory, the JavaScript interpreter embedded in the browser must accompany this pattern with information about its type, perhaps using additional bits to distinguish among the possible types. When the variable is accessed later in the program's execution, the bit pattern in memory is retrieved along with the additional bits, enabling the interpreter to recognize the data as a character.
With respect to data files, file extensions are commonly used to identify the type of data stored in that file. For example, a file with a .txt or .dat extension at the end is generally assumed to be a text file. Its contents are thus assumed to be characters, represented as either 8-bit ASCII or 16-bit Unicode sequences. Applications software will likewise utilize proprietary extensions to identify files formatted using that software's scheme, e.g., .docx for Microsoft Word or .pdf for Adobe's Portable Document Format.
FIGURE 9 illustrates how a computer can interpret the same bit pattern as representing different values, depending on context. You can enter up to 32 bits in the text box, then click to see how that bit pattern would be interpreted as a decimal integer, a single-precision floating-point value, or a sequence of ASCII characters.
FIGURE 9. Interactive Interpreter of 32-bit sequences.
✔ QUICK-CHECK 8.12: The ASCII table in FIGURE 6 shows that the binary sequence 01000001 represents the character 'A'. Use the interactive interpreter in FIGURE 7 to confirm this. What decimal value is represented by this code?
✔ QUICK-CHECK 8.13: The IEEE floating-point format reserves some bit patterns for representing special values. For example, a 32-bit pattern that begins with 011111111 has a special meaning. Using the interactive interpreter in FIGURE 7, determine what 011111111 followed by all zeros represents. What if a pattern other than all zeros follows 011111111?
Chapter Summary
- Data can be stored electronically in two ways, either as analog values (which can vary across an infinite range of values) or as digital values (which use only a discrete set of values).
- The primary trade-off between analog and digital data representation is variability vs. reproducibility — analog representations are ideal for storing data that is highly variable but does not have to be reproduced exactly.
- Because each bit of information on a computer is significant, modern computers are digital devices that store data as discrete, reproducible values. The simplest and most effective digital storage systems include two distinct (binary) states, typically referred to as 0 and 1.
- Any integer value can be stored as a binary number — a sequence of bits (0s and 1s), each corresponding to a power of 2.
- Most computers and programs employ a fixed-width integer representation, using a set number of bits (usually 32 bits) for each integer value. Using the two's-complement notation, bit patterns that begin with a 1 are interpreted as negative values.
- Any real number can be normalized into scientific notation, with all digits shifted to the right of the decimal place, e.g., 1234.5 → 0.12345 x 104.
- Using the IEEE floating-point standard, a real value is represented as a bit pattern consisting of the fractional and exponent components from its normalized form.
- ASCII (American Standard Code for Information Interchange) is a standard code for representing characters as 8-bit patterns. As computing becomes more and more international, ASCII is being replaced by Unicode, a 16-bit encoding system capable of supporting most foreign-language character sets.
- Because all types of data are stored digitally as bit patterns, any program that stores a piece of data in memory must remember its type to subsequently access and correctly interpret its meaning.
Review Questions
- TRUE or FALSE? The binary value 11012 represents the decimal number 27.
- TRUE or FALSE? The decimal number 100 is represented as the binary value 1101002.
- TRUE or FALSE? If the binary representation of a number ends with 1, it is an odd number.
- TRUE or FALSE? Using the two's complement notation for representing integers, any bit pattern starting with a 1 must represent a negative number.
- TRUE or FALSE? ASCII code is a program written to convert binary numbers to their decimal equivalents.
- Describe two advantages of storing data digitally, rather than in analog format.
- What decimal value is represented by the binary number 011010012? Show the steps involved in the conversion, then use the Data Representation Page to verify your answer.
- What is the binary representation of the decimal value 92? Show the steps involved in the conversion, then use the interactive interpreter in FIGURE 7 to verify your answer.
- It was mentioned in the chapter that having two representations of zero, both a positive zero and a negative zero, would be both wasteful and potentially confusing. How might the inclusion of both zeros cause confusion or errors within programs?
- Assuming that a string is stored as a sequence of ASCII codes corresponding to its individual characters, what string would be represented by the bit pattern 01001111011011110111000001110011?
- Suppose the bit pattern 001001100 appears at multiple places in a file. Will this pattern always represent the same value every time it appears? If not, why not?
