X6: Pages that Calculate

Chapter X5 introduced JavaScript features that enabled the development of fully interactive Web pages. You were able to enter text into the page via text boxes, then initiate events (e.g., by clicking on a button) that would access that text and integrate it into the page. For example, the invitation generator page (EXAMPLE 5.5) enabled you to customize an invitation by entering input values (recipient name, event description, and date) and those values would be incorporated into a custom invitation at the click of a button. While many Web-based applications involve inputting and processing text, there are many more that instead process numbers. For example, a page that calculates how much you should tip for a meal would require you to enter the check amount and the desired percentage. From those values, it could calculate the tip amount and display it in the page.

In this chapter, you will extend your capabilities by using numbers and mathematical operations to create Web pages that calculate. The number data type will be introduced, as well as some of JavaScript's predefined mathematical functions that can be used for more complex calculations.

      JavaScript Numbers

Each unit of information processed by a computer belongs to a general category, or data type, which defines the ways in which the information can be handled. In JavaScript, text values (sequences of characters enclosed in single quotes) are referred to as strings. In addition to the string data type, JavaScript values can also be numbers and Booleans (true/false values, which will be explored in a later chapter). Each JavaScript data type is associated with a specific set of predefined operators, which are part of the JavaScript language and may be used by programmers to manipulate values of that type. For example, we have already seen that strings can be glued (or concatenated) together using the + operator. Similarly, JavaScript predefines the standard arithmetic operators + (addition), - (subtraction), * (multiplication), / (division), and ** (exponentiation) for use with numbers.

Mathematical operators can be applied to numbers as well as variables that store numbers. FIGURE 1 below shows several examples of assignments to variables using math operators.

In mathematics, the symbol = is used to indicate equality. Thus, a statement such as z = z + 1; wouldn't make much sense in an algebraic context. However, you must remind yourself that JavaScript uses = to assign values to variables, rather than to determine equality. The expression on the right-hand side of an assignment is first evaluated using the current values of any variables. Then, the value of that expression is assigned to the variable on the left-hand side of the assignment. In the example z = z + 1; the result is that the variable z has its value increased by 1. It may help to think of = as the gets operator. When you read the statement z = z + 1; think if it as saying that "z gets z + 1." This reading emphasizes the directionality of an assignment: the variable on the left-hand side is being assigned the value of the expression on the right-hand side.

When working with JavaScript numbers, it may help to know the following:

1. To improve readability, JavaScript automatically displays very large or very small values using scientific notation. In this format, values are written as numbers between 1 and 10 multiplied by 10 to a particular power. For example, if you attempted to display the number 1000000000000000000000000 in a page, the number would be displayed as 1e24, symbolizing 1 x 10²⁴.
2. Like most programming languages, JavaScript stores all numbers in memory locations of a fixed size: 64 bits, to be exact. As a result, only a finite range of numbers can be represented in JavaScript. For example, 1e308 (which represents a one followed by 308 zeros!) can be represented in JavaScript, but 1e309 cannot. If you try to evaluate 1e309, the value will be treated as "Infinity." Similarly, 1e-323 is representable, but 1e-324 is rounded down to 0.
3. Even within its potential range of numbers, JavaScript cannot represent all possible values. Between any two real numbers lie infinitely more numbers, so representing all of them on a finite computer is impossible. Instead, JavaScript can represent approximately 16 significant digits (ignoring leading and trailing zeros). For example, JavaScript represents the number 0.9999999999999999 (with 16 9s to the right of the decimal) exactly, but 0.99999999999999999 (with 17 9s) is rounded up to the value 1.

    1 + (2 * 3)      (1 + 2) * 3      9 / 2      4**2      5e2 + 3

      Number Boxes

In Chapter X5, you used text boxes to read and process characters typed by you. There is nothing to stop you from entering a number into a text box, accessing that box's contents and incorporating it into the page (as before). However, a text box is not ideal for inputting numbers for several reasons. First, there is no error checking with a text box. If you intend to enter a number but add an extraneous character (e.g. 1q2 when you meant 12), the browser will let you. However, an error will occur when you try to apply a mathematical operator to something that is clearly not a number. Second, even if you enter a number in a text box, it will be treated as a string when accessed using the value attribute. This can lead to subtle errors when performing mathematical operations.

Fortunately, HTML provides another type of input element that is specifically designed for entering numbers. A number box is like a text box, except that its type attribute is assigned to be "number" instead of "text":

    <input type="number" id="ELEMENT_ID">

Recall that text boxes had optional attributes that could be used to initialize it contents and resize the box. The value attribute works the same for number boxes — if you assign a number value to the value attribute, that number will appear in the box when the page is loaded. The size attribute, however, does not work to resize number boxes. The equivalent effect can be obtained by assigning the min and max attributes, with their values designating the intended smallest and largest values for that box. If you assign numbers to min and max, the number box will appear wide enough to fit that range of numbers. For example, the following number box would initially contain the number 1024 and would be wide enough to fit 9 digits.

    <input type="number" id="numBox" min=0 max=999999999" value=1024>

Number boxes have a new attribute, valueAsNumber, which is used to access the number in the box. For example, if you entered 10 in a number box named numBox, then numBox.valueAsNumber would evaluate to the number 10 (not the string '10').

The HTML document in EXAMPLE 6.1 contains a number box, with id id="numBox". In the DoubleIt function, that number entered in the box is accessed using numBox.valueAsNumber, and its double is displayed.

While a number box also has a value attribute, you should avoid using it when accessing the contents since value always evaluates to a string. For example, if you entered 10 in a number box named numBox, then numBox.value would evaluate to the string '10' (not the number 10).

    Simplifying Computations with Variables

The HTML document in EXAMPLE 6.2 serves as a simple tip calculator. The resulting page contains two number boxes in which you can enter the check amount and the tip percentage. The boxes are wide enough to accommodate the range of values specified by the min and max attributes (7 characters wide for amountBox and 3 characters wide for percentBox). Since amountBox does not have a value attribute, it will initially be empty. The percentBox will contain the default value 20. When the button is clicked, the Calculate function is called to calculate and display the tip amount using the numbers from the boxes. Note that the tip amount will display using as many decimal places as needed. This looks odd, since dollar amounts are typically rounded to two decimal places, denoting cents. You will learn how to adjust this shortly.

Chapter X5 introduced variables as names that store values. By assigning the contents of a text box to a variable, that succinct variable name could be used in complex expressions which simplified the code. For example, in EXAMPLE 6.2, the variables amount and percent were assigned to store the numbers from the text boxes, which simplified the display message. In addition to serving as shortcuts for text or number box contents, variables are also useful for temporarily storing the results of computations. For example, we could use a variable to store the result of the tip calculation, then use that variable to simplify the output message even further. This is done in EXAMPLE 6.3.

Another advantage of using variables to store the results of a computation is that it simplifies formatting that result when displaying it. The suffix .toFixed(#) can be added to a variable to round the number to a fixed number of decimal places. The desired number of decimal places is specified in the parentheses (in place of #). In EXAMPLE 6.3, the variable tip is formatted so that the number is rounded to two decimal places: tip.toFixed(2). This has the effect of displaying the number in a dollar and cents format.

    Example: Compound Interest

Suppose you have decided to invest in your future. You have a certain amount of money to invest, say $1000.00, and a long-term investment account that would pay yearly interest, say 3.5%. The first year of your investment, you would earn $35.00 in interest, giving you a total of $1035.00 in the account. In the second year, you would earn 3.5% interest on this new total, giving you $36.22 in interest for a total of $1071.22. After 10 years, your $1000 investment will grow to $1410.60.

The formula for calculating the compound interest on an investment is as follows:

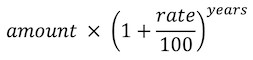
where amount is the amount to be invested, rate is the yearly interest rate, and years is the number of years for the investment. The HTML document in EXAMPLE 6.4 implements this computation. The resulting Web page has three number boxes in which you can enter the amount, rate and years. At the click of the button, the numbers are accessed and assigned to variables, and those variables are used in computing the final amount after accumulating compound interest. Note that the ** operator is used to raise a value to a power, and the .toFixed(2) suffix is used to round the amounts to two decimal places.

      JavaScript Math Functions

In mathematical terms, a function is a mapping from some number of inputs to a single output. The math operators we have previously seen, e.g., +, -, *, / and **, are symbols that denote functions. For example, the + operator takes two inputs and calculates their sum (1 + 2 → 3). Similarly, the ** operator takes two numbers and calculates the first raised to the power of the second (2**3 → 2³ → 8).

In addition to these built-in operators, JavaScript provides an extensive library of predefined mathematical functions (FIGURE 2). All these functions begin with the prefix Math., which signifies that function is part of a library of mathematical functions.

From a programmer's point of view, a function can be viewed as a unit of computational abstraction. When you call the Math.sqrt function in the following JavaScript statement:

    root = Math.sqrt(12.25);

you do not need to know the computational steps involved in performing the calculation of the square root. You simply apply the predefined Math.sqrt function and it produces the desired result (Math.sqrt(12.25) → 3.5). With this perspective in mind, we will often refer to applying a function to inputs as calling that function. We will also refer to the output of the function as the return value for the function call.

FIGURE 3 shows an interactive visualizer, where you can select the math function, enter number(s) in the box(es), and see the result of that function call. For example, the first default is a call to the Math.sqrt function with input 1024. When you click on the button to the right, the value returned by that call (Math.sqrt(1024) → 32) is displayed below. You can enter different inputs in the number box or even select a different function using the pull-down menu. Likewise, the second default displays the result of the function call Math.max(-1.2, 2) → 2.

EXERCISE 6.8: Predict what each of the following function calls would return, then use the visualizer in FIGURE 3 to confirm your answers.

    Math.abs(-33)    Math.ceil(2.8)    Math.floor(2.8)    Math.round(2.8)    Math.min(8, 2)
    

The HTML document in EXAMPLE 6.5 includes four different calls to math functions. The page calculates the maximum of two numbers using Math.max, the difference between the numbers using Math.abs, and the square roots of the numbers using Math.sqrt.

  <!doctype html> <!-- Applies Math functions to numbers | Dave Reed --> <html lang="en"> <head> <title> Numbers </title> <script> function Process() { num1 = num1Box.valueAsNumber; num2 = num2Box.valueAsNumber; maxNum = Math.max(num1, num2); diff = Math.abs(num1 - num2); root1 = Math.sqrt(num1); root2 = Math.sqrt(num2); outputP.innerHTML = 'The maximum of the two is ' + maxNum + '<br>' + 'The difference between them is ' + diff + '<br>' + 'Their square roots are ' + root1 + ' and ' + root2; } </script> </head> <body> <h2>JavaScript Math Functions</h2> <p><label for="num1Box">Enter two numbers:</label> <input type="number" id="num1Box" min=-99999 max=99999 value=25> and <input type="number" id="num2Box" min=-99999 max=99999 value=30></p> <button onclick="Process();">Process</button> <hr> <p id="outputP"></p> </body> </html>

EXERCISE 6.9: Confirm the behavior of this page by clicking on the See in Browser button using the default values 100 and 64. Experiment with different numbers in the boxes.

Add functionality to the page by having it also display the minimum of the two numbers.

    Example: Distance Between Points

A function call can appear anywhere in a JavaScript expression. When an expression containing a function call is evaluated, the return value for that call is substituted into the expression. For example, in the assignment below, the return value of the function call Math.sqrt(25) has 1 added to it, resulting in the variable being assigned 6.

    addNum = Math.sqrt(25) + 1;

The HTML document in EXAMPLE 6.6 contains more complex function calls. The resulting page has number boxes where you can enter the x and y coordinates of two points, and it then calculates the distance between those points using the formula:

It uses the ** to square the coordinate differences and Math.sqrt to take the square root of their sum.

  <!doctype html> <!-- Calculates the distance between two points | Dave Reed --> <html lang="en"> <head> <title> Point Distance </title> <script> function ShowDistance() { x1 = x1Box.valueAsNumber; y1 = y1Box.valueAsNumber; x2 = x2Box.valueAsNumber; y2 = y2Box.valueAsNumber; xDiffSquared = (x1-x2)**2; yDiffSquared = (y1-y2)**2; distance = Math.sqrt(xDiffSquared + yDiffSquared); outputP.innerHTML = 'The distance between (' + x1 + ', ' + y1 + ') and (' + x2 + ', ' + y2 + ') is ' + distance; } </script> </head> <body> <h1>Point Distance</h1> <p>Enter the coordinates of two points.</p> <p><label for="x1Box">Point 1:</label> (<input type="number" id="x1Box" min=-9999.9 max=9999.9 value=0>, <input type="number" id="y1Box" min=-9999.9 max=9999.9 value=0>) </p> <p><label for="x2Box">Point 2:</label> (<input type="number" id="x2Box" min=-9999.9 max=9999.9 value=3>, <input type="number" id="y2Box" min=-9999.9 max=9999.9 value=4>) </p> <button onclick="ShowDistance();">Click for Distance</button> <hr> <p id="outputP"></p> </body> </html>

EXERCISE 6.10: Confirm the behavior of this page by clicking on the See in Browser button using the default coordinates (0,0) and (3,4).

Add functionality to the page by having it also display the minimum of the two numbers.

      Random Numbers

Recall that a function is a mapping from some number of inputs to a single output. According to this definition, a function can require zero inputs, as demonstrated by the simple user-defined functions from Chapter X4. Those functions accessed any values they needed directly from text boxes. Similarly, the predefined JavaScript function Math.random that takes no inputs but returns a useful result. Every time Math.random is called, a different random number between 0 (inclusive) and 1 (exclusive) is returned. In other words, it returns a random value from the range [0, 1), with the smallest possible value that may be returned being 0 and the largest possible value being very, very close to 1.

For example, the following statements would assign random numbers from the range [0, 1) to the variables randy1 and randy2:

    randy1 = Math.random();

    randy2 = Math.random();

Since each call to Math.random produces a different random number from the range, the two variables would be assigned different values as a result of these assignments.

 

Designer Secrets

If we are being technically precise, we should say that the Math.random function returns a pseudo-random number in the range 0 (inclusive) to 1 (exclusive). The value returned by the function is not completely random — it uses a complex algorithm that utilizes numerous factors (including the current time in milliseconds) to select a number that appears random. If you knew the details of the algorithm and the exact values it used, it would be possible to predict the value that would be returned by the function. However, these details are not available to the programmer or the user, so the effect is that the values returned by Math.random appear random.

 

By itself, the Math.random function is not incredibly useful — there are not very many applications that require a random number between 0 and 1. However, a call to Math.random can be placed in an expression to adjust the range of the numbers. For example, the expression

    2*Math.random()

would evaluate to a random number in the range [0..2). One way to see this is to consider the extreme values obtainable from Math.random. The smallest value that Math.random() can return is 0 — if that number is doubled, you still have 0. The largest value that Math.random() can return is 0.999999... — if that number is doubled, you get 1.999999... Any values in between 0 and 1 would yield a number between 0 and 2 when doubled. Similarly,

    Math.random() + 1

would evaluate to a random number in the range [1..2). In general:

    X*Math.random() + Y

will yield a random number in the range [Y, X+Y). FIGURE 8 contains an interactive visualizer of this formula. You can enter values for X and Y in the boxes, then see a random number and the range that it is taken from.

Enter numbers for the expression involving Math.random(), then click the button to see the result.

* Math.random() +   Evaluate Expression

---

 

FIGURE 8. Interactive random expression visualizer.

EXERCISE 6.11: Confirm the behavior of this page by clicking on the See in Browser button using the default numbers 1 and 0. Experiment with this page to become familiar with the pattern. Predict what numbers would need to be entered in the boxes to generate a random number from each range:

    [0, 100)      [5, 10)      [2, 3)      [100, 200)      [0.5. 2.5)

 

Common Errors to Avoid

Because the Math.random function does not require any inputs, you might be tempted to leave off the parentheses when attempting to call it. Although such an omission does not generate an error, the resulting behavior is far from that of the intended call. Without the parentheses, a function name is treated like a variable and evaluates to the function definition. Thus, the assignment

    num = Math.random;

would assign the variable num to the function itself. The parentheses after the function name are required if the intent is to call the function and use its returned output. For example, the following statement calls the Math.random function and assigns the returned random number to num.

    num = Math.random();

 

    Example: Pick-4 Lottery

Consider a Pick-4 lottery that utilizes four bins of numbered balls, each containing the same number of balls numbered starting at 1. If there are 10 balls in each of the bins, numbered 1 to 10, then 10⁴ = 10,000 different Pick-4 combinations can potentially be picked. Increasing the number of balls significantly increases the number of possible combinations, which significantly decreases a person's odds of winning. For example, if there are 30 balls to choose from in each bin, labeled from 1 to 30, then 30⁴ = 810,000 different number combinations could be selected.

If we want to simulate picking a random ball out of a bin, we will need an expression that picks a random integer from the range 1..numBalls. As we learned above, the expression:

    numBalls*Math.random() + 1 

will yield a random real number in the range [1, numBalls+1). If we took the result of this expression and rounded down, we would then produce a random integer between 1 and numBalls, as desired:

    Math.floor(numBalls*Math.random() + 1)

The HTML document in EXAMPLE 6.7 that uses this expression to simulate selecting random balls. The resulting page has a box where you can enter the number of balls. When the button is clicked a random Pick-4 selection is displayed, along with the odds of winning.

  <!doctype html> <!-- Selects a Pick-4 lottery winner | Dave Reed --> <html lang="en"> <head> <title> Pick-4 Lottery </title> <script> function Lottery() { numBalls = numBox.valueAsNumber; pick1 = Math.floor(numBalls*Math.random() + 1); pick2 = Math.floor(numBalls*Math.random() + 1); pick3 = Math.floor(numBalls*Math.random() + 1); pick4 = Math.floor(numBalls*Math.random() + 1); numPossible = numBalls**4; percent = 100*(1/numPossible); outputP.innerHTML = 'The Pick-4 lottery winner is ' + pick1 + '-' + pick2 + '-' + pick3 + '-' + pick4 + '<br> BTW, your odds of winning are 1 in ' + numPossible + ' or ' + percent.toFixed(8) + '%.'; } </script> </head> <body style="text-align:center"> <h1>Pick-4 Lottery</h1> <p> <label for="numBox">Number of balls:</label> <input type="number" id="numBox" min=0 max=999 value=42> </p> <button onclick="Lottery();">Generate Pick-4 Winner</button> <hr> <p id="outputP"></p> </body> </html>

EXERCISE 6.12: Confirm the behavior of this page by clicking on the See in Browser button using the default number of balls (42). Are all the Pick-4 numbers between 1 and 42? Click on the button multiple times to confirm that the numbers are always within that range.

EXERCISE 6.13: What modifications would need to be made in the HTML document so that the balls are numbered starting at 0? That is, if there were 42 balls then they would be number 0 to 41. Make the modifications and confirm that it works as described.

      Putting It All Together

A variety of measures have been developed to characterize the readability of text. Usually, these measures describe readability in terms of grade level, e.g.,

This fairly simple sentence is rated at a sixth grade reading level.

One such measure is defined by the Flesch-Kincaid Grade Level Formula, which considers the average number of words per sentence and the average number of syllables per word:

    gradeLevel = 0.39*averageWordsPerSentence + 11.8*averageSyllablesPerWord - 15.59

For example, the above sentence consisted of 12 words with a total of 18 syllables. Thus, there are (12 / 1) = 12 words per sentence and (18 / 12) = 1.5 syllables per word. According to the Flesch-Kincaid Formula, the reading grade level for this text would be:

    gradeLevel = 0.39*12 + 11.8*1.5 - 15.59 = 6.8

We can automate the calculation of reading level using a Web page, in which you enter the number of sentences, words and syllables. At the click of a button, those values can be accessed and the reading level calculated:

The HTML document in EXAMPLE 6.8 implements this page.

  <!doctype html> <!-- Calculates the reading level of text | Dave Reed --> <html lang="en"> <head> <title> Flesch-Kincaid </title> <script> function GradeLevel() { sentences = sentencesBox.valueAsNumber; words = wordsBox.valueAsNumber; syllables = syllablesBox.valueAsNumber; avgWordsPerSentence = words/sentences; avgSyllablesPerWord = syllables/words; level = 0.39*avgWordsPerSentence + 11.8*avgSyllablesPerWord - 15.59; outputP.innerHTML = 'The Flesch-Kincaid Grade Level is ' + level.toFixed(1); } </script> </head> <body> <h1>Flesch-Kincaid Grade Level</h1> <p>This page calculates the Flesch-Kincaid Grade Level for a piece of text, using the forumla:</p> <p style="text-indent:0.4in"><i>Grade Level = 0.39*averageWordsPerSentence + 11.8*averageSyllablesPerWord - 15.59</i></p> <table> <tr><td><label for="sentencesBox">How many sentences?</label></td> <td><input type="number" id="sentencesBox" min=0 max=999999></td></tr> <tr><td><label for="wordsBox">How many words in the sentences?</label></td> <td><input type="number" id="wordsBox" min=0 max=999999></td></tr> <tr><td><label for="syllablesBox">How many syllables in the words?</label></td> <td><input type="number" id="syllablesBox" min=0 max=999999></td></tr> </table> <p><button onclick="GradeLevel();">Calculate Grade Level</button></p> <hr> <p id="outputP"></p> </body> </html>

There are several details to note about this document and how it implements the desired appearance and behavior of the page.

• Since there are three inputs that you must enter, all numbers, the page contains three number boxes. These boxes are given ids that describe their purpose: sentencesBox contains the number of sentences, wordsBox contains the number of words, and syllablesBox contains the number of syllables.
• In order to produce the desired behavior, the GradeLevel function must complete three logical tasks: (1) access the numbers in the boxes, (2) perform the calculations, and (3) display the results.
• Since there are three number boxes, there are three variables that are assigned to their contents. Note that the valueAsNumber attribute is used to access the numerical contents of the boxes. The names of the variables correspond naturally with the box ids.
• The formula for calculating the reading level is fairly complex. To simplify the code, two variables are used to store intermediate values (average number of words per sentence and average number of syllables per word). While the variable names (avgWordsPerSentence and avgSyllablesPerWord) are on the long side, they very clearly denote that value that is stored. The variables are then used to calculate the reading level and store it in a variable (level).
• Finally, the calculated reading level is displayed in the page by assigning a message to the innerHTML attribute of outputP. Note that the suffix .toFixed(1) is added to the variable. This ensures that the grade level is rounded to one decimal place (i.e., the nearest tenth) when it is displayed in the page.
• There are blank lines between the statements that carry out the three logical tasks in the function. These are not necessary and in fact are ignored by the browser (as is all excess whitespace). However, separating the individual tasks with blank lines makes the code easier to read and debug.

---

      Chapter Summary

• JavaScript has three basic data types: strings, numbers, and Booleans.
• The basic arithmetic operators + (addition), - (subtraction), * (multiplication), / (division) and ** (exponentiation) are provided for numbers. If the + operator is applied to a string and a number, the number is automatically converted into a string and then concatenated, e.g., '10' + 1 → '10' + '1' → '11'.
• For readability, JavaScript uses scientific notation to display very small and very large numbers.
• As numbers are stored in memory cells of fixed size, JavaScript can represent only a limited range of numbers. If numbers exceed a certain number of significant digits, they may be rounded off.
• A number box is like a text box, except that you can only enter only numeric values. The general form of a number box element is:

      <input type="number" id="BOX_ID" min=MIN_VAL max=MAX_VAL value=INIT_VAL> 

  If the optional min and max attributes are present, the number box will be automatically sized to fit that range.
• The value in a number box is accessed using its valueAsNumber attribute, e.g., numBox.valueAsNumber.
• JavaScript variables can be assigned values of any type, including numbers and mathematical expressions formed by applying operators to numbers.
• JavaScript variables are commonly used (1) as a shortcut for the contents of a text or number box, and (2) to temporarily store the results of computations.
• When an assignment statement is executed, the expression on the right-hand side is evaluated first, and the resulting value is assigned to the variable on the left-hand side.
• From a programming perspective, a function is a unit of computational abstraction — when calling a function, you do not need to understand the steps the function uses, you simply apply the desired function and obtain the result.
• JavaScript provides an extensive library of predefined mathematical functions, including square root (Math.sqrt), absolute value (Math.abs), maximum (Math.max), minimum (Math.min), round down (Math.floor), round up (Math.ceil), and round to the nearest integer (Math.round).
• The predefined Math.random function takes no inputs and returns a random real number taken from the range [0, 1).
• A call to Math.random can be embedded in an expression to generate numbers from different ranges.

---

      Projects

All projects should follow the basic design guidelines described in this and the previous chapters. These include:

• There should be a comment element near the top that includes your name and a brief description of the page. There should be well-defined head and body sections, with a title element in the head and all the visible elements in the body.
• Any complex action that takes place in the page should have a corresponding function defined in the head (in script tags). The statement(s) in the function should be indented and the name of the function should be descriptive of its purpose.
• If a function accesses the contents of a number box, it should do so via the valueAsNumber attribute and assign the value to a variable. Variables and text boxes should have descriptive names.
• For a complex computation, intermediate values can be calculated and assigned to variables.
• Each number box should have a label to its left, describing its purpose. If there are multiple number boxes, they should align.

PROJECT 6.A: Download a copy of the HTML document in EXAMPLE 6.8 (by clicking on the Download link) and save it on your computer under the name level.html. Next, modify the document so that, instead of calculating the grade level using the Flesch-Kincaid Formula, it instead using the Gunning Fog Formula (which assumes that any word of three or more syllables is complex):

    gradeLevel = 0.4*avgWordsPerSentence + 100*(numComplex/numWords)

The page should look similar to the page from EXAMPLE 6.9. That is, it should list the Gunning Fog Formula, it should have number boxes for the three values (number of sentences, number of words, and number of complex words), and a button click should display the grade level, rounded to the nearest tenth. Be sure to add your name to the comment element in the HTML document.

PROJECT 6.B: Recall from Chapter C1 that computer memory is comprised of individual bits of data. A bit (short for binary digit) can store one of only two values, commonly referred to as 0 and 1. However, using two bits, you can represent four different values through the bit patterns 00, 01, 10, and 11. With three bits, you can represent eight different values &mdash via 000, 001, 010, 011, 100, 101, 110, and 111. In general, N bits of memory enable you to represent 2^N different values.

Also recall that a byte consists of 8 bits. In other words, 8 bits will fit into 1 byte, 16 bits will fit into 2 bytes, and so on. If the number of bits is not a multiple of 8, then a portion of the last byte will be unused. Thus, 1-8 bits will fit into 1 byte, 9-16 bits will fit into 2 bytes, and so on.

Create a Web page named bits.html that contains a number box where can enter a number. At the click of a button, your page should calculate and display two values: (1) the number of values that can be represented using that number of bits and (2) the number of bytes those bits will fit into (as shown below).

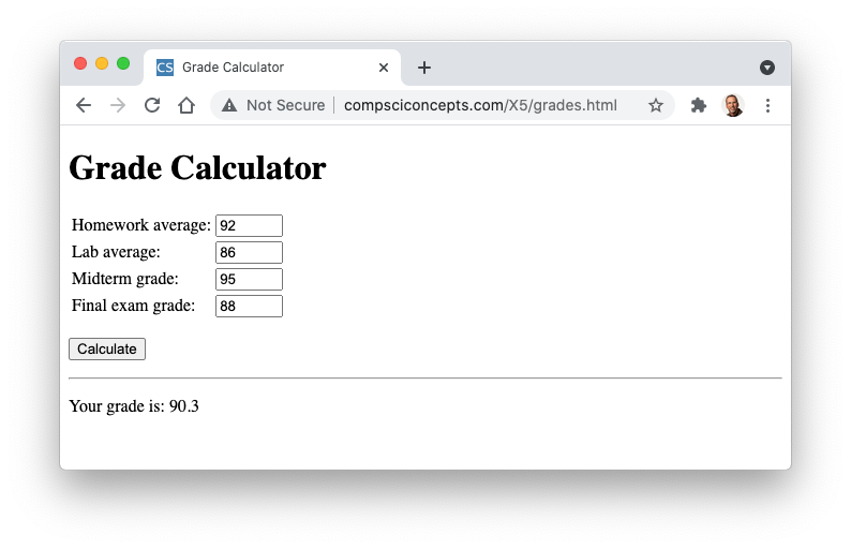
PROJECT 6.C: Consider the task of calculating a student's overall average for a course. Assume the course has a grading scheme with weighted averages for homework, labs, a midterm exam, and a final exam:

    Homework     25%
    Labs         20%
    Midterm      25%
    Final exam   30%

To calculate the overall course average, each individual grade is scaled by the appropriate factor and then added to produce the course average. Thus, if a student had a homework average of 92, a lab average of 86, a midterm exam score of 95, and a final exam score of 88, their course average would be:

	average = 92*(25/100) + 86*(20/100) + 95*(25/100) + 88*(30/100) = 90.35

Create a Web page named grades.html that can be used to calculate a student's overall average for a course. Your page should contain number boxes where you can enter your homework average, lab average, midterm exam score, and final exam score (as shown below). When the button is clicked, the grade level should be calculated and displayed, rounded to the nearest tenth of a point.

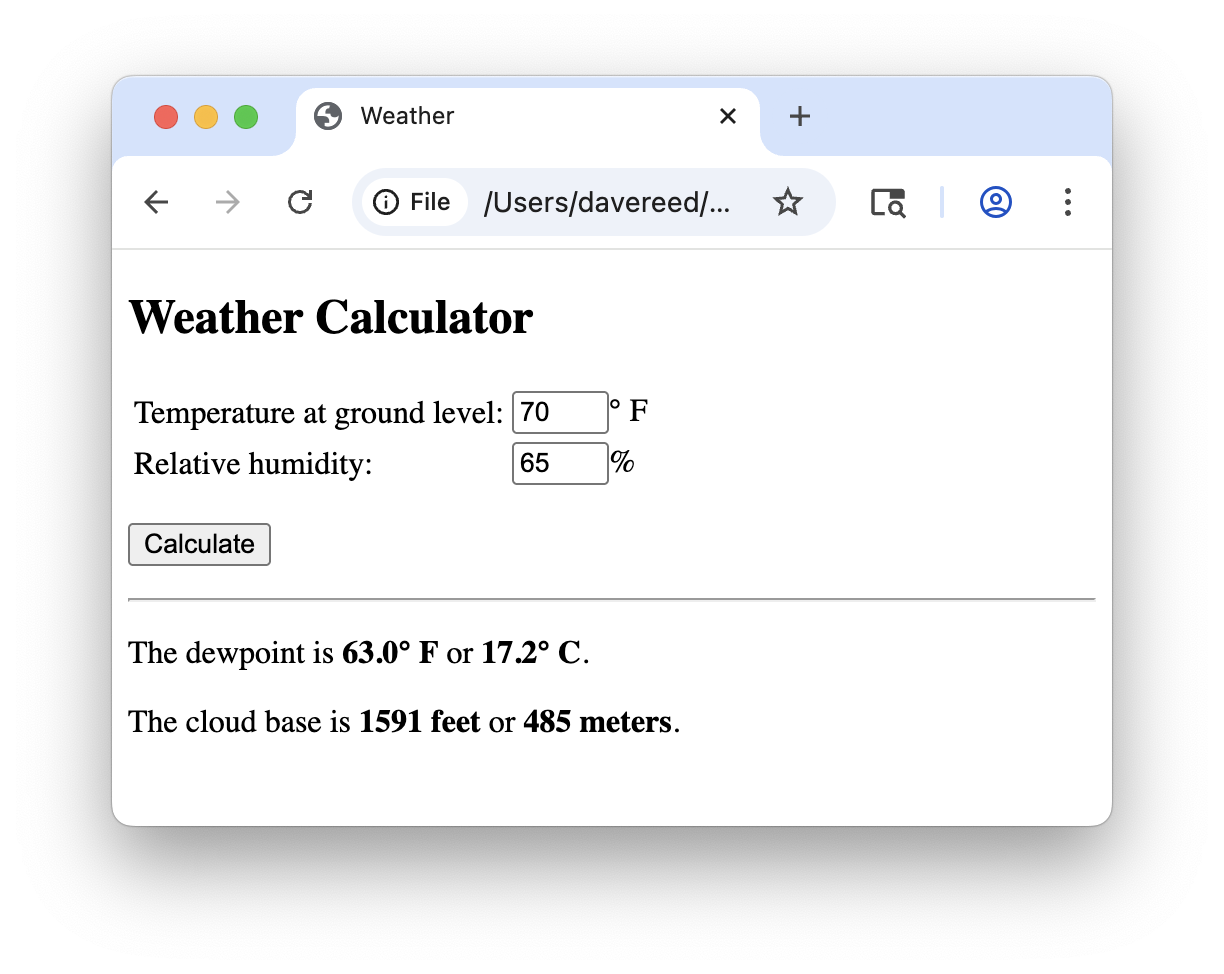
PROJECT 6.D: Weather reports often contain stats that describe current conditions. Two of these stats are dew point (the temperature to which the air must be cooled in order for water vapor to condense into water) and cloud base (the altitude at which clouds will form). Both of these stats can be easily calculated if you know the ground temperature (in degrees Fahrenheit) and the relative humidity:

    dewPoint = tempInF - (100-humidity)/5;
    cloudBase = 1000*(tempInF - dewPoint)/4.4;

The formulas calculate the dew point in degrees Fahrenheit and the cloud base in feet. If we wanted to also display those stats in Celsius and meters, we would need to know the conversion formulas:

    celsius = (fahrenheit - 32) * 5/9
    meters = feet / 3.28085

Create a Web page named weather.html that can be used to calculate the dew point and cloud base. Your page should contain number boxes where you can enter the ground temperature and relative humidity (as shown below). When the button is clicked, the dew point and cloud base should be calculated and displayed in both formats, rounded to the nearest tenth.