C6: Algorithms & Programming
When I am working on a problem, I never think about beauty. I think only of how to solve the problem. But when I have finished, if the solution is not beautiful, I know it is wrong. — R. Buckminster Fuller
A programming language is a system of notation for describing computations. A useful programming language must therefore be suited for both description (i.e., for human writers and readers of programs) and for computation (i.e., for efficient implementation on computers). But human beings and computers are so different that it is difficult to find notational devices that are well suited to the capabilities of both. — R.D. Tennant
The central concept underlying all computation is that of the algorithm, a step-by-step sequence of instructions for carrying out some task. When you interact with a computer, you provide instructions in the form of mouse clicks, menu selections, or command sequences. These instructions tell the computer to execute specific tasks, such as copying a piece of text or saving an image. At a more detailed level, when you write JavaScript statements, you are specifying instructions that the browser must follow to perform actions, such as accessing user input or displaying a message in the page.
Algorithms were introduced in Chapter C5, in the context of Computational Thinking. This chapter presents an overview of algorithms, their design and analysis, and their broader connection to computer science. After introducing techniques for solving problems, we provide several example algorithms for you to study, accompanying each with an interactive visualization that will enable you to experiment with the algorithm. We also discuss the evolution of programming languages and the advantage of using advanced languages to write computer algorithms at a high level of abstraction. After completing this chapter, you will be familiar with the steps involved in designing an algorithm, coding it in a programming language, and executing the resulting program.
Algorithms
Programming may be viewed as the process of designing and implementing algorithms that a computer (or a program executing on that computer) can carry out. The programmer's job is to create an algorithm for accomplishing a given objective and then to translate the individual steps of the algorithm into a programming language that the computer understands. For example, the JavaScript programs in Chapters X4-X10 contain statements that instruct the browser to carry out specific tasks, such as displaying a message or updating an image in the page. The browser understands these statements and is therefore able to carry them out, producing the desired results.
Algorithms in the Real World
The use of algorithms is not limited to the domain of computing. For example, a recipe for baking chocolate chip cookies is an algorithm. By following the instructions carefully, anyone familiar with cooking should be able to bake a perfect batch of cookies. Similarly, when you give someone directions to your house, you are defining an algorithm that the person can follow to reach that specific destination. Algorithms are prevalent in modern society because we are constantly faced with unfamiliar tasks that we could not complete without instructions. You may not know how long to cook macaroni and cheese or how to assemble a bicycle, so algorithms are provided (e.g., cooking instructions on the macaroni and cheese box, or printed assembly instructions accompanying the bike) to guide you through these activities.
Of course, we have all had experiences with vague or misleading instructions, such as recipes that assume the knowledge of a master chef or directions to a house that rely on obscure landmarks. For an algorithm to be effective, it must be stated in a manner that its intended executor can understand. If you buy an expensive cookbook, it will probably assume that you are experienced in the kitchen. Instructions such as "create a white sauce" or "fold in egg whites until desired consistency" are probably clear to a chef. On the other hand, the instructions on the side of a typical macaroni and cheese box do not assume much culinary expertise. They tend to be simple and precise, like those in FIGURE 1 (left). As you have no doubt experienced in developing interactive Web pages, computers are more demanding with regard to algorithm specificity than any human audience could be. Computers require that the steps in an algorithm be stated in an extremely precise form. Even simple mistakes in a program, such as misspelling a variable name or forgetting a semi-colon, can confuse the computer and render it unable to execute the program.
Specifying the solution to a problem in precise steps can be difficult, and the process often requires experience, creativity, and deep thought. However, once the problem's solution is designed and written down in the form of an algorithm, that problem can be solved by anyone capable of following the algorithm steps. The earliest surviving examples of written algorithms date back some four thousand years to the Babylonian civilization that inhabited present-day Iraq. Archeologists have discovered numerous examples of Babylonian clay tablets containing step-by-step instructions for solving mathematical and geometric problems (FIGURE 1, right).

FIGURE 1. Cooking instructions on a box of KRAFT® Macaroni and Cheese (Kraft Foods); Babylonian clay tablet, with mathematical algorithms written in cuneiform (British Museum, London, UK/Bridgeman Art Library).
✔ QUICK-CHECK 6.1: TRUE or FALSE? A sequence of instructions for assembling a bookcase does not qualify as an "algorithm," as the instructions are not written in formal, mathematical notation.
Algorithms and Computational Thinking
Chapter C5 introduced algorithms in the context of computational thinking. Recall the four characteristics that define computational thinking:
- DECOMPOSITION:
- Break the problem down into smaller, more manageable tasks.
- PATTERN RECOGNITION:
- Recognize how solutions to similar problems can be applied to new problems.
- ABSTRACTION:
- Focus on important details while ignoring irrelevant information.
- ALGORITHMS:
- Design and implement the solution in terms of an algorithm.
When solving a problem, the final step is formalizing the solution in the form of an algorithm. By doing so, anyone can subsequently apply that algorithm to solve the problem, without having to recreate the entire computational thinking process. Thus, a clearly stated algorithm is a blueprint for future problem solving, providing a new abstraction that simplifies solving related problems that may be encountered.
The example problem from Chapter C5, finding the tallest person in a room, is a good example of this. If you are tasked with finding the tallest person, you could simply apply one of the proposed algorithms (reproduced in FIGURE 2) to solve the problem. Beyond that, you could utilize pattern recognition to realize that many related problems could be solved by adapting these solutions. For example, if you needed to find the oldest person in a room (or the one whose birthday is closest, or the one who has visited the most countries, ...), you could easily adapt these algorithms to tackle similar tasks.
 |
 |
FIGURE 2. Algorithms for finding the tallest person in a room (from Chapter C5).
The task of finding the tallest person also demonstrates that most real-world problems can be solved in different ways. This means that multiple algorithms can be written to solve the same problem, often with tradeoffs in terms of simplicity or efficiency.
✔ QUICK-CHECK 6.2: TRUE or FALSE? For a precise, clearly stated problem, there can be only one algorithm that provides a solution.
Algorithm Analysis
When more than one algorithm have been developed to solve a problem, it is often desirable to determine which is better. Often, there is not a single correct answer: your choice for the "better" algorithm depends on what features matter to you. If you don't care how long it takes to solve a problem but want to be sure of the answer, it makes sense for you to favor the simplest, most easily understood algorithm. However, if you are concerned about the time or effort required to solve the problem, you will want to analyze your alternatives more carefully before deciding.
For example, consider the two algorithms that we have developed for finding the tallest person in a room. Algorithm 1 involves asking for each person's height and then comparing it with the height written on the page. Thus, the amount of time needed to find the tallest person using Algorithm 1 will be directly proportional to the number of people. If there are 100 people in line and it takes 10 seconds to compare heights, then executing Algorithm 1 will require 100 x 10 = 1,000 seconds. Likewise, if there are 200 people in line, then executing Algorithm 1 will require 200 x 10 = 2,000 seconds. In general, if you double the number of people, the time necessary to complete Algorithm 1 will also double.
By contrast, Algorithm 2 allows you to perform multiple comparisons simultaneously, which saves time. While the first pair of people compares their heights, all other pairs are doing the same. Thus, you can eliminate half the people in line in the time it takes to perform one comparison. This implies that the total time involved in executing Algorithm 2 will be proportional to the number of rounds needed to shrink the line down to one person. For example, if you start with 8 people, the first round of height comparisons eliminates half the people, leaving 4. The second round reduces that to 2, and the third round identifies the tallest person. If there were 16 people in the room, Algorithm 2 would require one additional round: 16 → 8 → 4 → 2 → 1.
In mathematics, the notion of a logarithm captures this halving effect: ⌈log2 N⌉ represents the number of times a value N must be halved before it reaches 1, where ⌈ ⌉ denotes rounding up to the next integer if necessary (FIGURE 3). Therefore, Algorithm 2 will find the tallest person in an amount of time proportional to the logarithm of the number of people. For example, if there are 100 people in and it takes 10 seconds to compare heights, Algorithm 2 will require ⌈log2 100⌉ x 10 = 7 x 10 = 70 seconds. If there are 200 people, then Algorithm 2 will require 10 x ⌈log2 200⌉ x 200 = 8 x 10 = 80 seconds. In general, if you double the number of people, the time required to execute Algorithm 2 will increase by the duration of one additional comparison.
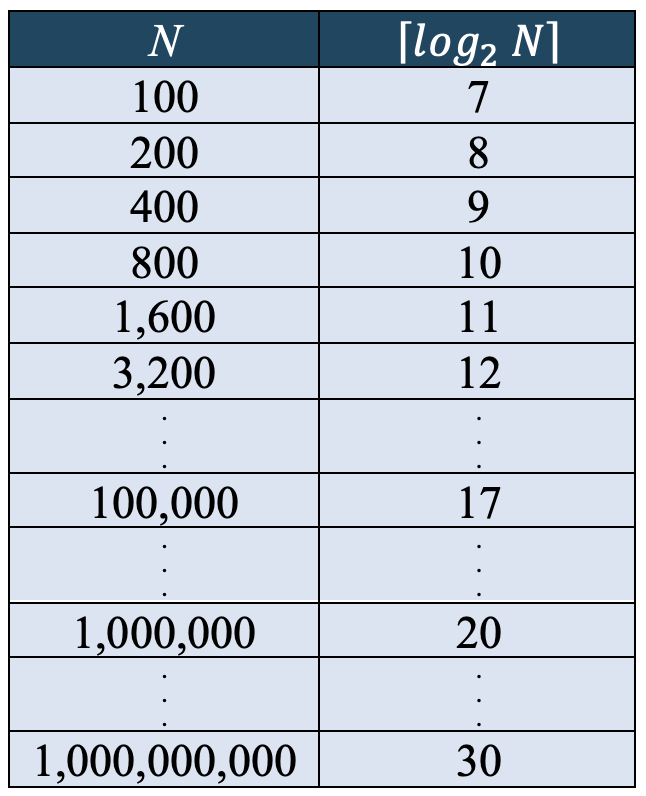
FIGURE 3. Table of logarithms (where ⌈⌉ denotes rounding up to the next integer).
It should be noted that the relative performance of these algorithms remains the same, regardless of how long it takes to complete an individual comparison. In the timings we have considered so far, we assumed that heights could be compared in 10 seconds. If a comparison instead took 20 seconds, you would still find that doubling the number of people doubles the time needed to perform Algorithm 1: 100 people would require 100 x 20 = 2,000 seconds, and 200 people would require 200 x 20 = 4,000 seconds. Likewise, doubling the number of people increases Algorithm 2's execution time by the duration of one additional comparison: 100 people would require ⌈log2 100⌉ x 20 = 7 x 20 = 140 seconds, and 200 people would require ⌈log2 200⌉ x 20 = 8 x 20 = 160 seconds.
✔ QUICK-CHECK 6.3: TRUE or FALSE? Algorithm 1 for finding the tallest person in a room will tend to be faster than Algorithm 2 when the number of people is large.
Big-Oh Notation
To represent an algorithm's performance in relation to the size of the problem, computer scientists use what is known as the Big-Oh notation. Executing an O(N) algorithm requires time proportional to the size of the problem, where N is a variable denoting the problem size. That is, if the problem size doubles, the time needed to solve that problem using the algorithm will also double. By contrast, executing an O(log N) algorithm requires time proportional to the logarithm of the problem size. That is, if the problem size doubles, the time needed to solve that problem increases by a constant amount. Based on our previous analysis, we can classify Algorithm 1 for finding the tallest person as an O(N) algorithm, where problem size N is defined as the number of people in the room. Algorithm 2, on the other hand, is classified as an O(log N) algorithm. The performance difference between an O(N) algorithm and an O(log N) algorithm can be quite dramatic, especially when you are contemplating extremely large problems.
It should be noted that the Big-Oh characterizations of Algorithms 1 and 2 in the previous paragraph focused on the time it takes to apply the algorithm. If we instead focused on the amount of work (i.e., the number of height comparisons), both algorithms would be considered O(N). This is obvious for Algorithm 1, but Algorithm 2 requires some analysis. In the first round, N/2 comparisons are made, then N/4, then N/8, and so on down to 1 comparison in the last round. The sum of N/2 + N/4 + N/8 + ... + 1 = N. So, in terms of work, Algorithm 2 is O(N), but the power of parallelism (carrying out multiple comparisons at the same time) makes it O(log N) in terms of time.
✔ QUICK-CHECK 6.4: TRUE or FALSE? If an algorithm is O(N), then doubling the problem size will double the amount of time needed.
Other Examples of Algorithms
The problem of finding the tallest person in a room is similar to a more general problem that occurs frequently in computer science. Computers are often required to store and maintain large amounts of data and then search through the data for specific values. For example, commercial databases typically contain large numbers of records, such as product inventories or payroll receipts, and allow the user to search for information on specific entries. Similarly, a Web browser that executes a JavaScript program must keep track of all the variables used throughout the program, as well as their corresponding values. Each time a variable appears in an expression, the browser must access the list of variables to obtain the associated value. Searching for an item in a list requires a systematic approach (e.g., an algorithm).
Sequential Search
The simplest algorithm for searching a list is sequential search, an approach that involves examining each list item in sequential order until the desired item is found.
Sequential search for finding an item in a list:
- Start at the beginning of the list.
- As long as the item has not been found, repeatedly:
- If that item is the one you are seeking, then you are done.
- If it is not the item you are seeking, then go on to the next item in the list.
- If you reach the end of the list and have not found the item, then it was not in the list.
This algorithm is simple and guaranteed to find the item if it is in the list, but its execution can take a very long time. If the desired item is at the end of the list or not in the list at all, then the algorithm will have to look at every entry before returning a result. Although sequentially searching a list of 10 or 100 items might be feasible, this approach becomes impractical when a list contains thousands or tens of thousands of entries.
In the worst case, sequential search involves checking every single entry in a list. This implies that the time required to locate a list item using sequential search is proportional to the size of the list. Thus, sequential search is an O(N) algorithm, where problem size N is defined as the number of items in the list (similar to Algorithm 1 above).
FIGURE 4 contains a sequential search visualizer. A list of 31 states is displayed. You can enter a desired state in the box, then click on the button to see each step in the search.
State abbreviation to be found:
FIGURE 4. Sequential search visualizer.
✔ QUICK-CHECK 6.5: Experiment with the sequential search visualizer. What is the minimum number of checks the algorithm can perform to find a particular state? For which state (or states) would this minimum occur? What is the maximum number of checks the algorithm can perform to find a state? For which state (or states) would this maximum occur?
✔ QUICK-CHECK 6.6: TRUE or FALSE? Suppose you have been given a sorted list of 100 names and need to find a particular name in that list. Using sequential search, it is possible that you might have to check every entry in the list before finding the desired name.
Binary Search
Fortunately, there is a more efficient algorithm for searching a list, binary search, but it can only be applied if the list adheres to some organizational structure. For example, entries in the phone book are alphabetized to help people find numbers quickly. If you were looking for "Dave Reed" in the phone book, you might guess that it would appear toward the back of the book, because 'R' is late in the alphabet. However, if you opened the book to a page near the end and found "Jackie Smith" at the top, you would know that you had gone too far and would back up some number of pages. In most cases, your knowledge of the alphabet and the phone book's alphabetical ordering system should enable you to home in on an entry after a few page flips.
Binary search follows this approach but in a more uniform way. Instead of selecting the place to check by guessing, binary search always selects the midpoint. As a result, each check reduces the range where the item could be by half.
Binary search for finding an item in an ordered list:
- Initially, the potential range in which the item could occur is the entire list.
- As long as the item has not been found, repeatedly:
- Identify the middle entry of the potential range.
- If the middle entry is the item you are seeking, then you are done.
- If the middle entry is greater than the item you are seeking, then reduce the potential range to those entries that come before the middle.
- If the middle entry is less than the item you are seeking, then reduce the potential range to those entries that come after the middle.
- If the potential range becomes empty, then the item was not in the list.
As step 2 consistently reduces the range in which the item could occur, repeating this step will eventually converge on the item (or reduce the potential range down to nothing, indicating that the item is not in the list). Since the range is cut in half after each check, there can be at most ⌈log2 N⌉ checks, where N is the number of entries in the list. Since the maximum number of steps required by binary search is proportional to the logarithm of the list size, binary search is an O(log N) algorithm (similar to Algorithm 2 above). For large lists, binary search will be much faster than sequential search. For example, a phone book for a small town (10,000 people) could be searched in at most ⌈log2 10,000⌉ = 14 checks, a large city (1 million people) in at most ⌈log2 1,000,000⌉ = 20 checks, and the entire United States (330 million people) in at most ⌈log2 330,000,000⌉ = 29 checks.
FIGURE 5 contains a binary search visualizer. The same sequence of states from FIGURE 4 is displayed (note that they are alphabetical order). As before, you can enter a desired state in the box, then click on the button to see each step in the search.
State abbreviation to be found:
FIGURE 5. Binary search visualizer.
✔ QUICK-CHECK 6.7: Experiment with the binary search visualizer. What is the minimum number of checks the algorithm can perform to find a particular state? For which state (or states) would this minimum occur? What is the maximum number of checks the algorithm can perform to find a state? For which state (or states) would this maximum occur?
✔ QUICK-CHECK 6.8: TRUE or FALSE? Suppose you have been given a sorted list of 100 names and need to find a particular name in that list. Using binary search, it is possible that you might have to look at every location in the list before finding the desired name.
Approximating a Square Root
As an example of a different type of algorithm, consider Newton's algorithm for calculating the square root of a number. Devised by Sir Isaac Newton (1643-1727) in the late 17th century, this simple algorithm can be stated as follows:
Newton's algorithm for finding the square root of N:
- Start with an initial approximation of 1.
- As long as the approximation isn't close enough, repeatedly:
- Refine the approximation using the formula:
newApproximation = (oldApproximation + N/oldApproximation)/2
You may note that step 2 of this algorithm is somewhat vague. Because some square roots (such as the square root of 2) cannot be represented as finite fractions, no algorithm can guarantee the exact square root. However, each successive approximation in Newton's algorithm is guaranteed to be closer to the square root. Thus, the person using the algorithm can determine exactly how close the approximation needs to be to suffice.
For example, suppose that we wanted to find the square root of 1,024. Newton's algorithm starts with the initial approximation 1. The next approximation is obtained by plugging 1 into the formula, producing a new approximation of (1 + 1,024/1)/2 = 1,025/2 = 512.5. The next approximation is (512.5 + 1,024/512.5)/2 = 514.5/2 = 257.25, followed by (257.2 + 1,024/257.2)/2 = 261.22/2 = 130.61, and so on. After only 11 refinements, the approximation is so close to the actual square root, 32, that a computer will round the value to 32.
1 → 1024
→ 512.5
→ 257.2490243902439
→ 130.61480157022683
→ 69.22732405448894
→ 42.00958563100827
→ 33.19248741685438
→ 32.02142090500024
→ 32.0000071648159
→ 32.0000000000008
→ 32
Analyzing the performance of Newton's algorithm is trickier than in previous examples, and a detailed investigation of this topic is beyond the scope of this book. The algorithm does converge on the square root in the sense that each successive approximation is closer to the square root than the previous one was. However, the fact that the square root might be a nonterminating fraction makes it impossible to define the exact number of steps required for convergence. In general, the algorithm tends to demonstrate logarithmic behavior, as the difference between a given approximation and the actual square root is cut roughly in half by each successive refinement.
FIGURE 6 contains a Newton's algorithm visualizer. You can enter a number in the box, then click on the button to see each refinement step. Note that you should not include commas when you enter a number in a box.
FIGURE 6. Newton's algorithm visualizer.
✔ QUICK-CHECK 6.9: How many refinements does Newton's algorithm require to compute the square root of 900? 10,000? 152,399,025?
Algorithms and Programming Languages
Programming is all about designing and coding algorithms for solving problems. The intended executor of those algorithms is the computer (or a program executing on that computer), which must be able to understand the instructions and then carry them out in order. Because computers are not very intelligent, the instructions they receive must be extraordinarily specific. Unfortunately, human languages such as English are notoriously ambiguous, and the technology for programming computers in a human language is still many years away. Instead, we write computer instructions in programming languages, which are more constrained and exacting than human languages are.
The level of precision necessary to write a successful program often frustrates beginning programmers. However, it is much easier to program today's computers than those of fifty years ago. As we explained in Chapter C4, the first electronic computers were not programmable at all — machines were wired to perform a certain computation. Although users could enter inputs via switches, the computational steps that the computer performed could be changed only by rewiring the physical components into a different configuration. Clearly, this arrangement made specifying an algorithm tedious and time-consuming. With the adoption of von Neumann's stored-program architecture, computers could be programmed instead of rewired. For the first time, computer engineers were able to write algorithms as sequences of instructions in a language understood by the computer, and these instructions could be loaded into memory and executed.
Machine & Assembly Languages
The first programming languages, which were developed in the late 1940s, provided a low level of separation from the hardware. Instructions written in these languages corresponded directly to the hardware operations of a particular machine. As such, they were called machine languages. Examples of machine language instructions might include:
- Move the value at main memory address 100 to register 3.
- Add 1 to the value in register 3.
- Jump to the instruction at main memory address 1024.
Of course, machine language instructions weren't represented as statements in English. As we learned in Chapter C1, computers store and manipulate data in the form of binary values (i.e., patterns of 0s and 1s). It is not surprising, then, that machine language instructions were also represented in binary. For example, the above instructions might be written as the bit patterns 0110011001000011, 1100000000010011 and 0101010000000000.
FIGURE 7 (left) shows a machine language program, with groupings of bits corresponding to the hardware operations of a particular computer. Although writing such a program and storing it in memory was certainly preferable to rewiring the machine, machine languages did not facilitate easy, intuitive programming. Programmers had to memorize the binary codes that corresponded to machine instructions, which was extremely tedious. Plus, entering in long sequences of zeros and ones was error prone, to say the least. If errors did occur, trying to debug a sheet full of zeros and ones was next to impossible. To make matters worse, each type of computer had its own machine language that correlated directly to the machine's underlying hardware. Machine language programs written for one type of computer could be executed only on identical machines.
In the early 1950s, programming evolved through the introduction of assembly languages. Assembly languages provide a slightly higher level of abstraction by allowing programmers to specify instructions using words (such as ADD or MOVE), rather than bit sequences. This certainly made the programmer's task simpler, as words were easier to remember and comprehend when reading and debugging a program. However, these words still corresponded to operations performed by the computer's physical components, so assembly language programming still involved thinking at a low level of abstraction. FIGURE 7 (right) shows the assembly language program that corresponds to the machine language program on the left.
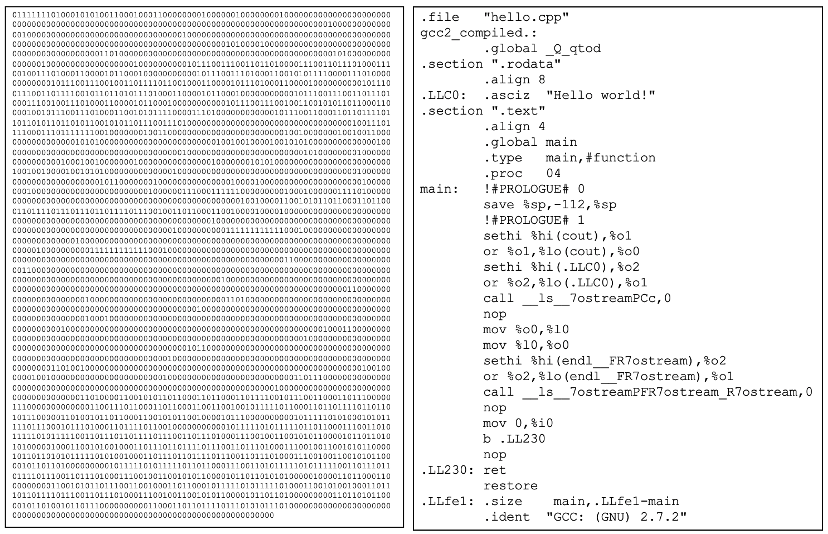
FIGURE 7. A machine language program (left) and corresponding assembly language program (right).
The introduction of assembly languages did not change the power of the computer itself — computers were still only capable of executing machine language instructions. A separate program, called an assembler, was required to translate assembly instructions into the corresponding binary machine language instructions. Thus, programming became a two-step process: (1) write the program in assembly language, then (2) translate that assembly language program into the equivalent machine language program using an assembler.
✔ QUICK-CHECK 6.10: TRUE or FALSE? One advantage of assembly languages over machine languages is that they enable the programmer to use words to identify instructions instead of using binary number sequences.
High-Level Languages
To solve complex problems quickly and reliably, programmers must be able to write instructions at a higher level of abstraction that more closely relates to the way humans think. When we solve problems, we make use of high-level abstractions and constructs, such as variables, conditional choices, repetition, and functions. A language that includes such abstractions provides a more natural framework through which to solve problems. Starting in the late 1950s, computer scientists began developing high-level languages to address this need. The first such language was FORTRAN, written by John Backus (1924-2007) at IBM in 1957. Two years later, John McCarthy (1927-2011) invented LISP at MIT, and a multitude of high-level languages soon followed. JavaScript, the high-level language introduced in Chapters X4-X10, was invented in 1995 by Brendan Eich (1964-) and his research team at Netscape Communications Corporation.
FIGURE 8 depicts two different high-level language programs that perform the same task: each asks the user to enter a name and then displays a customized greeting. The program on the left is written in JavaScript, and the one on the right is written in C++. As you can see, high-level programming languages are much closer to human languages than machine and assembly languages are. This makes writing programs and fixing errors much simpler.

FIGURE 8. High-level language programs (JavaScript and C++).
Another advantage of high-level languages is that the resulting programs are machine independent. Because high-level instructions are not specific to the underlying computer's hardware configuration, programs written in high-level languages are portable across computers. Such portability is essential, because it enables programmers to market their software to a wide variety of users. If a different version of the same program were required for each brand of computer, software development would be both inefficient and prohibitively expensive.
Not surprisingly, almost all software development today uses high-level programming languages, such as Python, C++, Java or JavaScript. However, it should be noted that machine and assembly languages have not gone away. As you will see in the next section, programs written in a high-level language must still be translated into the machine language of a particular computer before they can be executed. And in application areas where execution time is critical, say in controllers for jet stabilizers, modern programmers may still use assembly and machine languages to optimize the use of memory and the sequencing of instructions.
✔ QUICK-CHECK 6.11: TRUE or FALSE? JavaScript, C++, and Java are all examples of high-level programming languages.
Program Translation
While computers have become faster and more powerful over the last 80 years, they have not become any "smarter." Modern computers do not "understand" high-level programming languages — they still require programs to be written in binary machine languages in order to execute them. When a developer writes a program in a high-level programming language, that program must be translated into the machine language for that computer. Two basic approaches, known as interpretation and compilation, are employed to perform these translations.
The interpretation approach relies on a program known as an interpreter to translate and execute the statements in a high-level language program. An interpreter reads the program statements one at a time, immediately translating and executing each statement before processing the next one. This is, in fact, what happens when JavaScript programs are executed. A JavaScript interpreter is embedded in every modern Web browser. When the browser loads a page containing JavaScript code, the interpreter executes the code one statement at a time, displaying the corresponding output in the page (FIGURE 9).
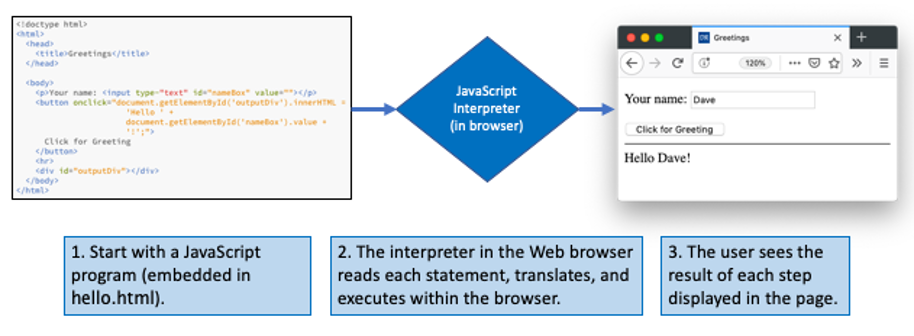
FIGURE 9. Interpreting a JavaScript program.
By contrast, the compilation approach relies on a program known as a compiler to translate the entire high-level language program into its equivalent machine language instructions. The resulting machine language program can then be executed directly on the computer (FIGURE 10). Most programming languages used in the development of commercial software, such as C and C++, employ the compilation technique.
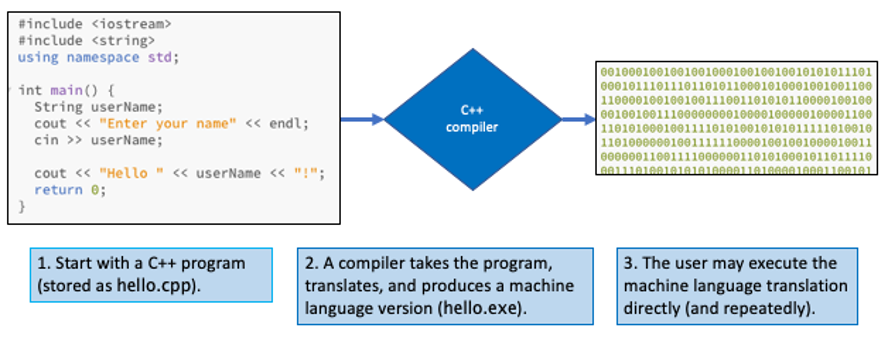
FIGURE 10. Compiling a C++ program.
There are trade-offs between the interpretation and compilation approaches. An interpreter starts producing results almost immediately, as it reads in and executes each instruction before moving on to the next. This immediacy is particularly desirable for languages used in highly interactive applications. For example, JavaScript was designed specifically for adding dynamic, interactive features to Web pages. If the first statement in a JavaScript program involves prompting the user for a value, then you would like this to happen as soon as the page loads, rather than waiting for the rest of the program to be translated. The disadvantage of interpretation, however, is that the program executes more slowly. The interpreter must take the time to translate each statement as it executes, so there will be a slight delay between each statement's execution.
A compiler, on the other hand, produces a machine language program that can be executed directly on the underlying hardware. Once compiled, the program will run very quickly. If a language is intended for developing large software applications, execution speed is of the utmost importance; thus, languages such as C++ are translated using compilers. The drawback to compilation, however, is that the programmer must take the time to compile the entire program before executing it.
It is interesting to note that these two approaches to program translation have analogous approaches to spoken and written language translation. To obtain real-time translation of a speech from one language to another (e.g., English to sign language), an "interpreter" is often used (FIGURE 11, top). This person stands on the stage, listens to the speaker, and provides the translation one sentence at a time. Since the translation is immediate, with a slight delay for the interpreter to process the words, the viewer can experience the speech and connect the words with the speaker's emotions and body language. If you want to read a book written in a foreign language, however, hiring an interpreter to read it to you sentence-by-sentence is clearly not practical. Instead, books are translated as a whole, by an expert that takes weeks or months to produce a copy of the book in the new language (FIGURE 11, bottom). While it takes time to do the entire translation, the translated book can be read and reread and can even be mass-produced for a wider audience. The person producing the translated book may be referred to as a "compiler."

FIGURE 11. A sign language interpreter (MSNBC); Shakespeare's Romeo and Juliet, translated into Polish, 1924 (CB Polona/Wikimedia Commons).
✔ QUICK-CHECK 6.12: TRUE or FALSE? When a Web page is loaded into a Web browser, JavaScript code in that page is executed by a JavaScript interpreter that is embedded in the browser.
Chapter Summary
- The central concept underlying all computation is that of the algorithm, a step-by-step sequence of instructions for carrying out some task.
- Programming may be viewed as the process of designing and implementing algorithms that a computer (or a program executing on that computer) can carry out.
- Algorithms are prevalent in modern society (e.g., cooking instructions, directions for assembling a bike), because we are constantly faced with unfamiliar tasks that we could not complete without instructions.
- Performance measures the speed at which a particular algorithm (or program designed to carry out that algorithm) accomplishes its task. Performance may be characterized by the number of steps involved or the time it takes to complete the task.
- Big-Oh notation is used to represent an algorithm's performance in relation to the size of the problem. An O(N) algorithm requires time proportional to the size of the problem, so doubling the problem size will roughly double the time required. An O(log N) algorithm requires time proportional to the logarithm of the size of the problem, so doubling the problem size only increases the time required by a constant amount.
- The sequential search algorithm, which can be used to find a particular item in a list, is an example of an O(N) algorithm, where N is the number of items in the list. Binary search, which can be used when the list is ordered, is an example of an O(log N) algorithm.
- Newton's algorithm is a simple, yet efficient, algorithm for approximating the square root of a number.
- Machine languages are low-level programming languages in which each instruction is a bit sequence that corresponds directly to a hardware operation of the machine.
- Assembly languages provide a slightly higher level of abstraction by allowing programmers to specify instructions using words, rather than bit sequences.
- High-level programming languages provide abstractions and problem-solving constructs that make problem solving simpler and more intuitive for the programmer.
- Before it can be executed on a computer, a program written in a high-level language must be translated into the machine language for that computer. This can be accomplished via an interpreter (which translates and executes each statement in the program in sequence) or a compiler (which translates the entire program into an equivalent machine language program).
Review Questions
- TRUE or FALSE? Big-Oh notation is used to measure the exact number of seconds required by a particular algorithm when executing on a particular computer.
- TRUE or FALSE? Binary search is an example of an O(log N) algorithm, where the number of items in the list to be searched is N.
- An algorithm must be clear to its intended executor to be effective. Give an example of a real-world algorithm that you have encountered and felt was not clear. Do you think that the algorithm writer did a poor job, or do you think that the algorithm was formalized with a different audience in mind? Explain your answer. Then, give an example of a real-world algorithm that you felt was clearly stated.
- Write an algorithm for directing a person to your house, apartment, or dorm from a central location. For example, if you live on campus, the directions might originate at a campus landmark. Assume that the person following the directions is familiar with the neighborhood or campus.
- Write an alternative algorithm for directing a person to your residence, but this time, assume that the person is unfamiliar with the area. How does this condition affect the way you describe the algorithm?
- Suppose that you have been given an O(N) algorithm that averages student grades, where N is the number of grades. If it takes 1 minute to average 100 grades using the algorithm, how long would you expect it to take to average 200 grades? 400 grades? Justify your answer.
- Suppose you needed to look up a number in your local phone book. Roughly, what is the population of your city? How many checks would be required, in the worst case, to find the phone number using sequential search? How many checks would be required, in the worst case, to find the phone number using binary search?
- Imagine that, while you are using Newton's algorithm, the approximations converge on the actual square root of the number. What would happen if you tried to further refine the square root? Would the value change? Why or why not?
- What is the difference between a compiler and an interpreter? What characteristics of an interpreter make it better suited for executing JavaScript programs?
