C9: Inside Multimedia
Music expresses that which cannot be put into words and that which cannot remain silent. — Victor Hugo
There is nothing worse than a sharp image of a fuzzy concept. — Ansel Adams
Chapter C8 explored how basic data types: integers, real numbers, characters and strings, could all be represented as sequences of bits. As we have seen throughout this book, however, computers can represent much more than numbers and text. Smart phones have the capability of recording dictation and converting spoken language into text. Digital cameras can capture and store photographs, which can then be manipulated by image processing software. Streaming services such as Netflix and Hulu provide movies and shows that can be downloaded and played on computers or smart televisions. Images, audio and video clips can be embedded in Web pages.
To store and manipulate complex data such as sound, images and video, computers require additional techniques and algorithms. Some of these algorithms allow the computer to convert data into binary, whereas others are used to compress the data, shortening its binary representation. This chapter builds upon the basic data representation ideas from Chapter C8 to explore methods of storing sound, images and video.
Representing Sound
Sounds are inherently analog signals. Each sound produces a pressure wave in the air with a unique amplitude (or height, usually measured in deciPascals) and frequency (duration over time). For example, FIGURE 1 compares the analog waveforms generated by a tuning fork, a violin, a piano, and a waterfall. When sound waves such as these reach your ear, they cause your eardrum to vibrate, and your brain then interprets that vibration as sound.
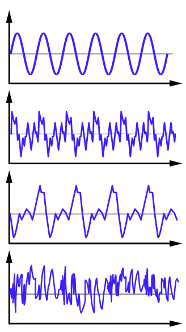
FIGURE 1. Waveforms corresponding to a tuning fork, violin, piano, and waterfall (Mike Run/Wikimedia Commons).
The practice of using analog signals to store and manipulate sounds began with the invention of the telephone by Alexander Graham Bell (1875), which was followed by Thomas Edison's phonograph (1877). Telephones translate a waveform into electrical signals of varying strengths, which are then sent over a wire and converted back to sound. Phonographs imprint waveforms as grooves of varying depth on the surface of a vinyl disk. Audio-cassette technology similarly represents waveforms as magnetic lines on a tape.
Recall the tradeoff between analog and digital representations as described in Chapter C8. An analog representation uses continuous values, meaning it can be measured to arbitrary precision. For example, an analog recording stored on a phonograph or cassette can produce high-quality sound if sensitive microphones and mixing equipment are used. The cost of this precision, however, is reproducibility. Since a phonograph or cassette stores the sound as a continuous waveform, copying that waveform exactly is problematic. Imagine you were given a drawing of a wavy line and asked to reproduce it — you might come very close but slight variations in the shape would be inevitable. Similarly, small errors will be introduced whenever the analog waveform stored on phonograph or cassette is copied. Typically, this is not a major concern because the human ear is unlikely to notice small inconsistencies in a sound recording. However, if a recording is duplicated repeatedly, then small errors can propagate. You may have noticed this if you have ever made a copy of copy of a cassette. Sound quality deteriorates as errors pile up during repeated recording. The sound quality of digital recordings may not be as high as analog, but they can be reproduced exactly. Thus, a digital music file can be copied over and over without any deterioration in sound quality.
To store sound digitally, its analog waveform must be converted to a sequence of discrete values. This is accomplished via digital sampling, in which the amplitude of the wave is measured at regular intervals and then stored as a sequence of discrete measurements. Each measurement records the amplitude of the wave at that fraction of a second. For example, FIGURE 2 shows a simple waveform with measurements of -60, 155, 150, 74, -70, -135, -148, 50, 92, 23, 4, 39, and 98 deciPascals. Once the measurements are taken, they can be stored as binary numbers in a file. The first commercial technology that stored sound files in a digital format was the Compact Disc (CD). Introduced in 1982, a CD can store up to 700 MB of music files, or approximately 80 minutes of digitally sampled sound.
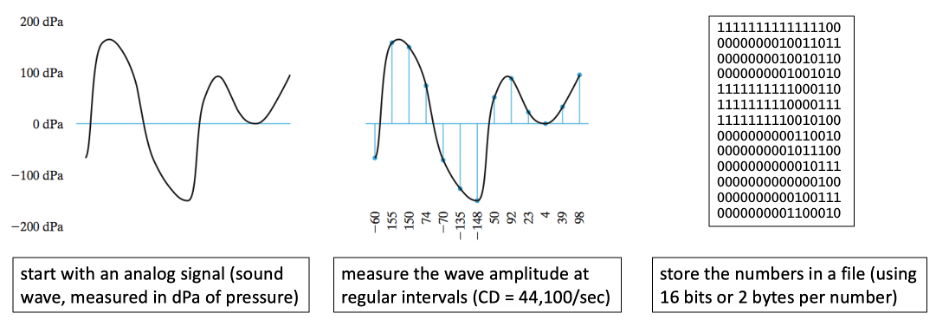
FIGURE 2. Digitizing and storing an analog sound wave.
To play a digital recording, a music player must extract the numbers and reconstruct the analog waveform (FIGURE 3). Since there are gaps between the measurements, the reconstruction may not be an exact reproduction of the original. The shorter the gap between measurements, the closer the reconstructed waveform will be to the original waveform. For a CD-quality recording, 44,100 measurements are taken each second, so most variations are too minute for the human ear to discern.
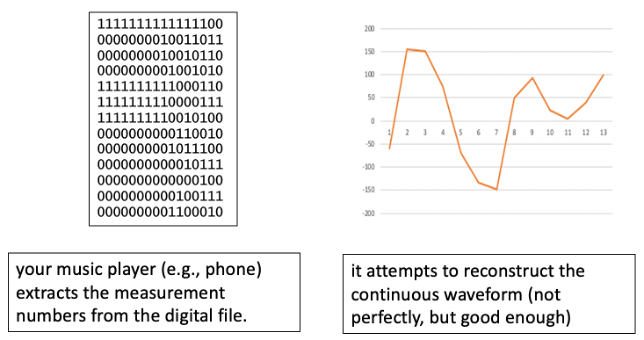
FIGURE 3. Playing a digital recording.
✔ QUICK-CHECK 9.1: TRUE or FALSE? In contrast to digital signals, analog signals use only a discrete (finite) set of values for storing data.
✔ QUICK-CHECK 9.2: TRUE or FALSE? Digital sampling is the process of measuring a waveform at regular intervals and storing the resulting discrete measurements.
Sound Compression
To reproduce sounds accurately, frequent measurements must be taken — 44,100 readings per second are required to achieve CD-quality sound. As a result, even short recordings can require massive amounts of storage. For example, consider the recording of a 3-minute song. Most songs utilize two independent tracks to obtain a stereo effect when played. Assuming each measurement is stored using 2 bytes (or 16 bits), that single song would require more than 31 MB (megabytes) of storage:
2 tracks x 180 seconds x 44,100 measurements/second x 2 bytes/measurement = 31.752 MB
Since the typical album contains 10-20 songs, storing an album could require 310-620 MB of storage. Thus, a CD, with a capacity of 700 MB is sufficient to store most albums.
With the popularity of smartphones and portable music players, the size of standard digital music files becomes problematic. If a phone has only 32 or 64 GB of storage, even a moderate library of albums would overwhelm its storage capacity. These file sizes would also make streaming difficult, as the time it would take to stream a 31 MB song would be considerable. For example, phones with 4G wireless connections can typically download around 1.5 MB per second. At that rate, downloading a single song would require 21 seconds and a 20-song album would require almost seven minutes. A 5G wireless connection can reduce those times by a factor of 10, which would still require around 40 seconds for the album download.
Fortunately, techniques have been developed to reduce the size of digital sound files, such as filtering out sounds beyond the range of human hearing or recognizing when a sound on one track will drown out a weaker sound on the other. The MP3 format, for example, uses techniques such as these to achieve a 75-95% reduction in size. Thus, a 3-minute song recording could be reduced from 31 MB to as little as 1.5 MB, allowing it to be downloaded on 4G wireless in only a second. Likewise, a 20-song album could be reduced from 620 MB to 31 MB, which could be downloaded in 21 seconds. Using a 5G connection, that would require only 2 seconds, which appears almost instantaneous to the user. The price for the impressive compression that the MP3 format achieves, however. is in sound quality. MP3 is known as a lossy format since information is lost in the compression. When as music player decompresses the file, that lost information will translate into discrepancies from the original waveform and lower overall sound quality. The MP3 format is widely used with portable music players and music streaming services, where reduced file size and download time is worth the slight drop in sound quality. In addition to MP3, a variety of proprietary audio formats have been developed by companies for distributing online music. For example, Apple uses a variant of the MP3 format (named AAC) for music it distributes via Apple Music.
It is interesting to note that the development of efficient algorithms for compressing and storing sound files have led to massive changes in the music industry. Before the release of the CD in 1982, music piracy (i.e., the illegal copying of a song or album) was not feasible on a large scale. Most individuals did not have the ability to physically duplicate a phonograph disk, and copying cassette recordings significantly reduced sound quality as errors were introduced. With the introduction of the CD and inexpensive devices for duplicating CDs, a person could mass produce copies, infringing on the rights of the artists and music companies. The development of compression formats, such as MP3 in 1993, reduced file sizes to the point that portable music players and smartphones could serve as the primary music source for most people. It also led to the creation and growth of the streaming music industry, starting with the Apple iTunes store in 2003 and subscription services such as Spotify (2006) and YouTube Music (2015). FIGURE 4 shows how streaming services have changed the music industry, accounting for almost 70% off all revenue in 2024.
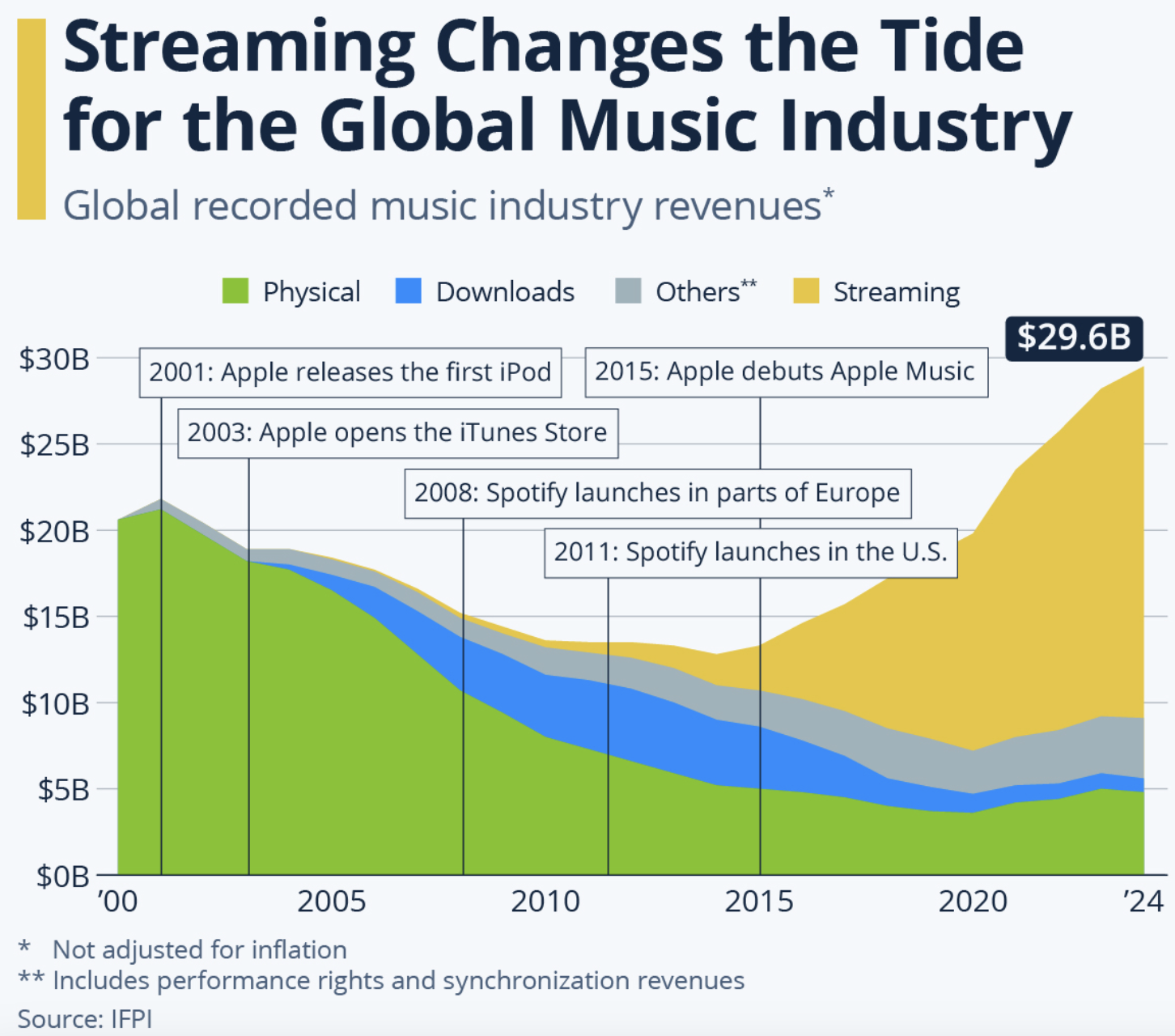
FIGURE 4. The growth of streaming services in music industry revenue (Statista).
✔ QUICK-CHECK 9.3: TRUE or FALSE? MP3 is known as a lossless format since no information is lost during the compression.
✔ QUICK-CHECK 9.4: Suppose you needed to download a 10-minute audio recording. If the recording is stored in CD-quality, it would require roughly 106 MB. How long would it take to download the recording using a wireless 4G connection (at 1.5 MB/sec)? Using MP3, that recording could be reduced to as little as 530 KB. How long would it take to download it using the same 4G connection?
Representing Images
Like sounds, images are inherently analog. In the real world, colors can appear with infinite variability. Film photography produces an analog representation of an image using chemical processes. When a film coated in silver halides is exposed to light, the chemical composition of the film is changed based on the frequency and intensity of the light source. Essentially, the film captures an analog representation of the image, which can then be developed to produce a photograph.
Analog images can be captured and stored digitally using a variety of formats. The simplest image format, a bitmap, digitally samples the colors in an image in much the same way that sound waveforms are sampled. A bitmap partitions the image into a two-dimensional grid of dots called pixels (short for picture elements) and then converts each pixel into a number. In the case of black-and-white pictures, each pixel can be represented as a single bit: 0 for a black pixel and 1 for a white pixel. For example, FIGURE 5 shows how a simple black-and-white image can be partitioned into an 8x8 grid (64 pixels) and then stored using 64 bits. It should be noted that the partitions in this example are large, resulting in some pixels that are part white and part black. When this occurs, the pixel is usually assigned a bit value corresponding to the majority color, so a partition that is mostly black will be represented as a 0.
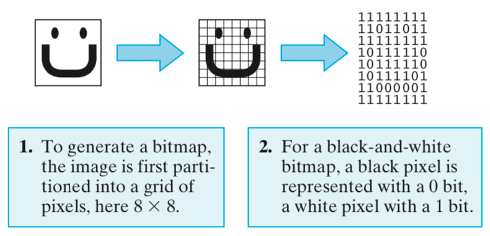
FIGURE 5. Sampling a black and white image to generate a bitmap.
Resolution is a term that refers to the sharpness or clarity of an image. Because each pixel is assigned a distinct value, bitmaps that are divided into smaller pixels will yield higher-resolution images. However, every additional pixel increases the necessary storage by one bit. FIGURE 6 illustrates this by comparing the same picture at four different levels of resolution. When stored using 72 pixels per square inch, as shown on the left, the image looks sharp. Each subsequent image in the series has half the resolution (36 pixels per square inch, 18 pixels per square inch, and 9 pixels per square inch) and so requires half the storage. As the resolution is reduced, however, the image quality is likewise reduced.

FIGURE 6. An image stored with reduced resolution from left to right.
While images such as the cat in FIGURE 6 are sometimes referred to as black-and-white images, they contain more than just black and white pixels. The more accurate term to describe these images is grayscale, since they contain a range of gray values (ranging from white to black). Typically, 256 different shades of gray can be represented in a grayscale image, requiring 8 bits of storage per pixel.
When storing a color image, even more bits per pixel are required due to the wider range of color values. The most common system translates each pixel into a 24-bit code, known as that pixel's RGB value. The term RGB refers to the fact that the pixel's color is decomposed into different intensities of red, green, and blue. Eight bits are allotted to each of the component colors, allowing for intensities ranging from 0 to 255 (with 0 representing a complete lack of that color and 255 representing maximum intensity). FIGURE 7 lists the RGB values for some common HTML colors. Note that some shades of red, such as darkred and maroon, are achieved by adjusting the intensity of a single component. Other colors, such as crimson and pink, require a mixture of all three component colors. Because each color component is associated with 256 possible intensities, 2563 = 16,777,216 different color combinations can be represented. Color bitmaps require 3 times more storage than grayscale bitmaps (24 vs. 8 bits per pixel), and 24 times more storage than black-and-white bitmaps (24 vs. 1 bit per pixel).
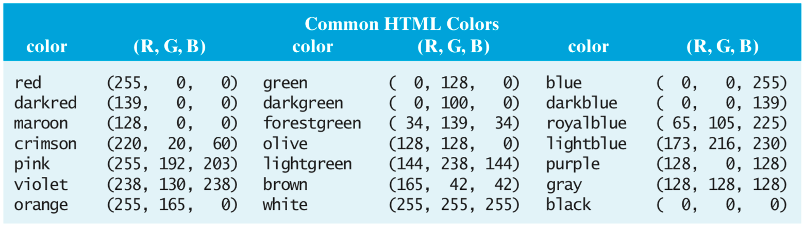
FIGURE 7. Common HTML colors and their (R, G, B) representations.
It is interesting to note that gray is denoted by the RGB value (128, 128, 128). In fact, any color for which the R, G, and B intensities are identical will be a shade of gray. At the extremes, (0 ,0, 0) is black, while (255, 255, 255) is white. Other shades fall in between, such as light gray (211, 211, 211) and dim gray (105, 105, 105).
FIGURE 8 contains an interactive color visualizer, in which you can enter RGB values (0-255 each) and see the corresponding color. There are two such visualizations, side-by-side, so that you can easily compare colors. Initially, the visualization shows dark green (0, 100, 0) and forest green (34, 139, 34).
| R: G: B: | R: G: B: |
FIGURE 8. Interactive RGB color visualizer.
✔ QUICK-CHECK 9.5: Using the color visualizer from FIGURE 8, display two colors that differ by one number in the blue component. For example, you might set the RGB values to (34,139,34) and (34,139,35). Can you tell the difference between these two colors? If not, how large of a difference does there need to be for you to differentiate the colors?
✔ QUICK-CHECK 9.6: TRUE or FALSE? In a bitmap, the number of pixels used to represent an image affects both how sharp the image appears and the amount of memory it requires.
✔ QUICK-CHECK 9.7: TRUE or FALSE? A 1200x800 color bitmap will require three times the storage of a 1200x800 grayscale bitmap.
Image Compression
Although bitmaps are simple to describe and comprehend, they require considerable memory to store complex images. For example, a photograph taken with a digital camera might contain as many as 48 megapixels, or 48 million pixels. If each pixel requires 3 bytes, then a single photograph would require 144 MB of space. Fortunately, formats have been developed, similar to the MP3 format for sound, that compress images so that they can be stored using less space. The three most common image compression formats on the Web are GIF (Graphics Interchange Format), PNG (Portable Network Graphics), and JPEG (Joint Photographic Experts Group). All three formats apply algorithms that shorten an image's bit-pattern representation, thus conserving memory and reducing the time it takes to transmit the image over the Internet.
The GIF format (introduced in 1987) uses techniques that identify repetitive patterns in an image and store those patterns more efficiently. For example, the bottom left corner of the cat picture (FIGURE 6) happens to be a 10x10 square of pixels that are all the same color. Instead of storing each of the 100 identical pixel RGB values, the GIF format would store the RGB value once along with information denoting the corners of the rectangle. This simple change could save thousands of bits of storage. In addition, if that or any other pattern occurred multiple times in the image, then it could be stored once along with a special marker substituted for each occurrence. Depending on the type of image, it is not uncommon for the GIF format to yield a 25-50% reduction in size when compared with a bitmap representation.
While the GIF format has been used extensively on the Web, it has its limitations. Since the format indexes each pixel using only 8 bits, a GIF image can display at most 256 different colors. In addition, legal questions surround the use of the format because of patents on parts of its compression algorithm. The PNG format (1995) was designed to improve upon the features of GIF and also avoid any patented techniques. It greatly expands the color range of images, allowing up to 64 bits per pixel. In addition, it uses more sophisticated compression techniques than GIF, which can further reduce the size of images (commonly 10% to 50% smaller than GIF).
GIF and PNG are known as lossless formats, as no information is lost during the compression. This means that the original image can be recovered exactly. Conversely, JPEG (1992) is a lossy format, as it employs compression techniques that are not fully reversible. For example, JPEG might compress several neighboring pixels by storing their average color value. In a color photograph, where color changes tend to be gradual, this approach can greatly reduce the necessary storage for an image — by as much as 90-95% — without noticeably degrading the image's quality. In practice, the GIF and PNG formats are typically used for line drawings and other images with distinct boundaries where precision is imperative; the JPEG format is most commonly used for photographs, where precision can be sacrificed for the sake of compression.
In addition to the bit patterns representing individual pixels, image formats such as GIF, PNG, and JPEG store additional information, or metadata, in the image file. For example, a digital image stored in one of these formats might contain metadata identifying its dimensions, the date it was created, and even the model and serial number of the camera or digital scanner that created it. This information can be useful for managing collections of digital images, such as organizing images by date or location. Metadata has also been used as evidence in criminal cases involving copyright violations, assisting authorities in identifying the origin of a photograph.
 Steganography
Steganography
An interesting side topic related to digital images is steganography — the practice of concealing a secret message in another message or object. Suppose you had a message that you wanted to send to a friend without anyone knowing. One option would be to utilize encryption (see Chapter C7) to encode the message and then text or email the encoded message. One drawback of this approach is that an observer might intercept that message and, even if they couldn't decode it, they would know that communication took place. Alternatively, you might embed that secret message in an image and post the image on social media. To a casual observer, the image would appear to be innocent, e.g., a vacation photo. Only your friend would know to look for and extract the hidden message.
The images below look identical to the human eye. However, the image on the right has been changed to embed a secret message. First, the message was broken down into a bit sequence using ASCII codes (see Chapter C8). Then, each bit of the message was inserted into the rightmost bit of the RGB code for a pixel. As we saw in EXERCISE 9.5, the human eye cannot distinguish between two colors whose RGB values differ by a single bit, so the image appears unchanged to the casual viewer. For a person in the know, however, those bits can be extracted and the message reconstructed from the public image.


If you are curious as to what the secret message is, download a copy of the image on the right to your computer. Then, go to the Website https://stylesuxx.github.io/steganography/ and upload the image. Select "Decode" to extract the secret message.
✔ QUICK-CHECK 9.8: What is the secret message hidden in the vacation photo example?
✔ QUICK-CHECK 9.9: TRUE or FALSE? Lossless compression formats tend to produce smaller files than lossy formats.
Representing Video
In principle, a motion picture is nothing more than a sequence of still images, or frames. By displaying the frames sequentially at a rate faster than the human eye can distinguish, the illusion of continuity is achieved. The first motion pictures were created in in the 1890's, capturing still images on celluloid photographic film. FIGURE 9 shows several frames from a black-and-white motion picture. Each frame is an image of a scene taken a fraction of a second later than the previous frame. A projector shines an intense light through the film and displays the frames at the appropriate rate (typically, 24 frames per second) to produce the moving images on a screen.
Since a traditional motion picture consists of a sequence of photographs on film, which are themselves analog representations of individual frames, it is an analog representation. In the 1970's, digital movie cameras and storage formats were developed that allowed for digitizing the moving image. The term video began to be used more extensively at that time, as motion pictures moved from being large film reels in canisters to digital files on computers.


FIGURE 9. Individual frames of a motion picture film (National Library of Medicine/Wikimedia Commons); a 1905 ad for a projector (Optical Lantern and Cinematograph Journal/Wikimedia Commons).
As was the case with images, there are numerous digital formats that may be used to store video. The simplest format would be to store each individual frame as a digital image, using an image format such as JPEG. Unfortunately, the storage requirements for such a simple representation would be unmanageable. For example, a high definition (HD) video utilizes 1920x1080 resolution, resulting in more than 2 million pixels per frame. Using the JPEG format, a single frame would require approximately 500 KB of storage. Since videos play 24 frames per second, a two-hour movie would require:
120 minutes x 60 seconds/minute x 24 frames/second x 500 KB/frame = 86.4 GB
Thus, a single movie could exceed the storage capacity of a smartphone or portable video player. Even a laptop could only store a few movies before filling the hard drive, and streaming would be virtually impossible due to the time it would take to download movies.
Video Compression
Fortunately, efficient compression formats have been developed for storing digital video. The most common format on the Web, known as MPEG or MP4, utilizes complex algorithms to take advantage of similarities between successive frames. For example, note that the frames in FIGURE 9 are very similar, since there is very little movement in the 1/24th of a second from one frame to the next. One person's hand or mouth may move slightly, but their legs remain stationary as they talk face-to-face. The background of the frames, depicting a wall, does not change at all in these frames. After storing the initial frame in its entirety, the MPEG format need only store the changes in each successive frame. For example, the second frame could be represented by identifying which small rectangles contain movement relative to the first frame, and only those rectangles would need to be stored. Since most of a frame will be unchanged from the previous one, this can greatly reduce the amount data that must be stored. While the compression rate depends on the contents of the video, storing a two-hour video in roughly 500 MB (or roughly 3 KB per frame) is common using the MPEG format. Note that this is roughly 0.6% of the basic, uncompressed format described above.
Elements of the MPEG format are included in the ATSC (Advanced Television Systems Committee) standard that is used for digital television broadcasts. Other related video compression formats are DVD, used for storing standard movies, and Blu-ray, used for storing high-definition movies.
 ASCII Movies
ASCII Movies
As a child, you may have encountered or even created flip books. A flip book consists of a series of drawings that differ by a small amount from page to page. By flipping quickly between the pages, the drawings appear to animate. Essentially, each drawing serves as a frame in the animation and the rapid flipping motion serves as a projector, showing each frame in succession so that the human eye perceives motion. The Web equivalent of a flip book is an ASCII movie. In an ASCII movie, each frame is a drawing made using characters from the keyboard. A Web page can then take those character-based frames and display them in succession to produce a moving picture.
The windows below enable you to create and display text-based movies. The frames of the ASCII movie are entered on the left, separated with the divider '====='. When the button is clicked, the movie defined by those frames is displayed to the right, with a 0.2 second delay between frames. Several sample movies are provided, ranging from the default 2-frame jumping jack figure to complex scenes. The links at the bottom allow you to load and display the provided movies, but you can also create your own!
Enter the frames below, separated by "=====". |
|
| Or select a pre-made movie: Jumping Jacks, Wink Wink, Free Throw, Pirate Ship | |
✔ QUICK-CHECK 9.10: Create your own ASCII movie in the above tool. Each frame should be "drawn" using characters from the keyboard, and the frames should be separated by five consecutive equals signs (i.e., =====).
✔ QUICK-CHECK 9.11: TRUE or FALSE? In most motion pictures, the differences from one frame to the next tend to be small and localized.
Chapter Summary
- Data can be stored electronically in two ways, either as analog values (which can vary across an infinite range of values) or as digital values (which use only a discrete set of values).
- Sound, images, and video are all inherently analog: sound is transmitted via a continuous waveform, colors are continuous in frequency and variability, and video is essentially a sequence of analog images.
- Digital formats have been developed for storing and reproducing sounds, images, and video.
- Before a sound can be stored digitally, its analog waveform must be converted to a sequence of discrete values via digital sampling.
- The MP3 format reduces the size of sound files by using a variety of techniques, such as filtering out sounds that are beyond the range of human hearing or are drowned out by other, louder sounds.
- Digital sound formats led to major changes in the music industry, including increased music piracy after the introduction of the CD and streaming music services after the development of MP3 and other compression formats.
- The simplest digital format for representing images is a bitmap, in which a picture is broken down into a grid of picture elements (pixels) and the color or intensity of each pixel is represented as a bit pattern.
- Each pixel in a color image can be represented by its RGB value — a triple measuring the red, green and blue intensities of that pixel.
- The three most common image formats on the Web, GIF (Graphics Interchange Format), PNG (Portable Network Graphics), and JPEG (Joint Photography Experts Group), start with a bitmap representation and then employ different methods of compressing the image.
- GIF and PNG are known as lossless formats, as no information is lost during the compression. Conversely, JPEG is a lossy format, as it employs compression techniques that are not fully reversible.
- Steganography is the practice of concealing a secret message in another message or object, such as embedding text within an image.
- A motion picture consists of a sequence of still images, or frames, that are displayed in rapid succession to produce the illusion of movement.
- The MPEG, or MP4, digital video format uses a variety of compression techniques, including some borrowed from JPEG, to compress movies.
Review Questions
- TRUE or FALSE? GIF and JPEG are examples of formats for representing and storing sounds.
- TRUE or FALSE? A phonograph is an example of a digital format for storing sound.
- TRUE or FALSE? The RGB value (255, 0, 0) denotes a bright blue color.
- TRUE or FALSE? Embedding a secret message in the pixels of an image is an example of steganography.
- Suppose that a library has a taped recording of a historically significant speech. What advantages would there be to converting the speech to digital format?
- How many different music formats do you regularly listen to (e.g., phonograph, CD, cassette tape, MP3)? Rank the different formats in terms of sound quality. Are you able to discern the quality differences when listening?
- What is the difference between a lossless format and a lossy format for storing digital images? For what type of images might one or the other be preferable?
- Consider a color photograph taken by an 8-megapixel camera. Without compressions, how big would you expect the image file to be? How big would the corresponding JPEG file be, assuming 90% compression?
- Is the MPEG compression format for storing video lossy or lossless? How did you determine your answer?
- Estimate the average number of bytes per frame for an MPEG file you own. That is, divide the size of the file by the approximate number of frames (you may assume 24 frames per second). Is this average consistent across different movie files?
