C5: Scientific & Computational Thinking
We live in a society exquisitely dependent on science and technology, in which hardly anyone knows anything about science and technology. — Carl Sagan
Computational thinking has a wide application beyond computing itself. It is the process of recognizing aspects of computation in the world and applying tools and techniques from computing to understand and reason about natural, social and artificial systems and processes. — Assessing Computational Thinking Across the Curriculum (Julie Mueller, Danielle Beckett, Eden Hennessey and Hasan Shodiev)
Chapter C4 provided an overview of the history of computers and computer science. This chapter provides a broader perspective, looking at the history of science and the role that scientific thinking plays in our lives. Science may be defined as "a system of knowledge covering general truths or the operation of general laws" (Merriam-Webster dictionary). It is important to our daily lives because science advances our understanding of the world and our place in it. In addition, scientific advances lead to practical applications that improve our quality of life, such as improvements in medicine that extend our lives, agricultural developments that yield abundant food, and new technology that allows us to learn and communicate across the world.
A full history of science and recognition of its many contributors are clearly beyond the scope of this book. This chapter provides a very brief overview of the history of science, beginning with the natural philosophers of ancient Greece up to the present day. The role of Galileo, as the father of modern science and originator of the scientific method is highlighted, along with other key pioneers. Scientific thinking, using experimentation as part of the scientific method, is described with examples of its use in understanding natural phenomena. Closely related to scientific thinking, computational thinking — a problem-solving approach that involves expressing problems and their solutions in ways that a computer could execute — is also described and a detailed example provided.
A (Very) Brief History of Science
The roots of science extend to before written history began, when the first humans observed nature and tried to understand its behavior. Modern science, as we think of it today, traces its roots back to the natural philosophers of ancient Greece. Thales (6th century B.C.) is recognized as one of the first philosophers to break from the use of mythology to explain nature, instead using hypothesis and theory to describe natural phenomena such as weather and astronomy. His scientific philosophy influenced many of the great minds that followed, including Plato (4th century B.C), who proposed a grand theory of cosmology that included heavenly bodies moving in uniform circles around the earth. Oddly, Plato believed that observation was confused and impure, and that truth could only be found through abstract contemplation. For example, he assumed that planets had circular orbits, since circles represented divine geometric perfection. Plato's pupil, Aristotle (FIGURE 1), went on to study cosmology, physics, biology, anatomy and logic, and is remembered for proposing a coherent, common-sense view of the natural world that dominated thinking for more than 2,000 years. Aristotle placed a greater value on observation as part of natural philosophy than did Plato, but his approach still did not include experimentation as a means of verifying or refuting theories. As a result, Greek natural philosophy is often referred to as pre-scientific, since it relied on contemplation and observation, but not experimentation.

FIGURE 1. Aristotle tutoring Alexander the Great, 1866 engraving by Charles Laplante (Wikimedia Commons).
The Roman civilization that dominated the western world after the conquest of Greece in the 2nd century B.C. built upon the tradition of Greek natural philosophy. Notable figures in Roman pre-science were Pliny (1st century) who categorized and described plants, animals and minerals, Galen (2nd century) who studied human anatomy and physiology, and Ptolemy (2nd century) who revised Aristotle's cosmology to match observations of planetary motion. As a whole, though, the Romans are better known for engineering than theoretical science. Building on the theories of the Greeks, they advanced the design and construction of roads, bridges, buildings, and aqueducts that enabled the expansion of their empire.
After the fall of Rome in 476, the so-called Dark Ages befell much of Europe. In western Europe, Greek knowledge was lost as population dropped due to plague and literacy virtually disappeared. In eastern Europe, Greek knowledge was suppressed by orthodox Christianity in the Byzantine Empire, which lasted until 1453. Fortunately, the legacy of Greek pre-science continued in other regions of the world. Europe's Dark Age was contrasted by the Islamic Golden Age (7th-13th centuries), during which the Islamic Empire covered parts of Europe, northern Africa, the Middle East, and western Asia. Greek writings were preserved by Arab scholars, and advances in astronomy, biology, and mathematics continued in the Greek tradition. In fact, the term algorithm, which is central to computer science today, is named after the 9th century Persian scholar and mathematician Muhammad ibn Musa al-Khwarizmi (FIGURE 2). Scientific development occurred independently in other parts of the world as well, most notably in China with its rich history in mathematics, medicine and agronomy, and in India with its history in mathematics, astronomy and metallurgy.

FIGURE 2. Muhammad ibn Musa al-Khwarizmi, detail of a 1983 USSR stamp (Wikimedia Commons).
Starting in the 11th century, a series of religious wars known as the Crusades took place between Christian Europe and the Islamic Empire. As waves of Crusaders invaded the Mediterranean and Middle East, Greek knowledge was rediscovered and brought back to Europe. In conjunction, Greek and Latin texts that had been preserved in monasteries were retrieved, leading to renewal of learning in Europe during the 12th century. Monastic schools and medieval universities formed, eventually leading to the European Renaissance of the 14th-16th centuries. The Renaissance was a cultural and intellectual revolution that was derived from the rediscovery of Greek thought, and encompassed widespread political reform, artistic expression, and the rise of humanism. One of the most notable figures of the Renaissance was Leonardo da Vinci (1452-1519), who could reasonably be described as a scientist, mathematician, engineer, architect, inventor, anatomist, botanist, painter, sculptor, musician and writer. Johannes Gutenberg's invention of the printing press in 1439 was key to the increase in literacy and the rapid spread of knowledge during this period.
✔ QUICK-CHECK 5.1: TRUE or FALSE? Greek natural philosophy is often referred to as "pre-scientific," since it relied on contemplation and/or observations, but not experimentation.
✔ QUICK-CHECK 5.2: During the Dark Ages, the scientific knowledge of the Greeks was lost throughout the entire world.
Modern Science
The intellectual upheaval of the Renaissance, including the Protestant Reformation, new world exploration, and widespread literacy, produced a cultural environment that allowed for questioning religious and scientific dogma. The ensuing Scientific Revolution of the 16th-17th centuries led to a world view in which the universe was thought of as a complex machine that could be understood through careful observation and, more importantly, experimentation. The revolution began with Nicolaus Copernicus (1473-1543) and his sun-centered cosmology, which deviated from the Aristotelean model that had dominated thinking for millennia. Johannes Kepler (1571-1630) refined that model to use elliptical instead of circular orbits. Galileo Galilei (1564-1642) pioneered the use of experimentation to validate observational theories, and as a result is considered by many to be the father of modern science. Galileo (Figure 3) used experimentation to lay the foundation of modern physics, studying motion, gravity and inertia as well as inventing the thermometer and other scientific instruments. He also founded modern astronomy, using a telescope to record precise observations and championing the Copernicus/Kepler model of cosmology (despite religious persecution). Another key figure in the Scientific Revolution was Isaac Newton (1642-1726), who formulated the laws of motion and universal gravitation, which formed the dominant scientific viewpoint for more than 200 years. He also contributed to numerous advances in astronomy and mathematics, including the invention of calculus.

FIGURE 3. Portraits of Leonardo da Vinci (self-portrait), Nicolaus Copernicus (by Mikolaj Kopernik), Galileo Galilei (by Justus Susterman) and Isaac Newton (by Godfrey Kneller) (Wikimedia Commons).
The Scientific Revolution established science as the preeminent source for the growth of knowledge. During the 19th century, science became professionalized and institutionalized through the growth of scientific societies, government sponsorship of scientific research, and universities as centers of scientific exploration. Continuing through the 20th century and to this day, scientists from around the world have advanced our understanding of nature through the scientific method. These include key figures in biology such as Louis Pasteur (1822-1895) who discovered the principles of vaccines, microbial fermentation, and pasteurization, and James Watson (1928-) and Francis Crick (1916-2004) who mapped the structure of DNA; key figures in chemistry such as John Dalton (1766-1844) who proposed the atomic theory of matter, and Dmitri Mendeleev (1834-1907) who constructed the periodic table of elements; and key figures in physics such as James Clerk Maxwell (1831-1879) with the theory of electromagnetism, and Albert Einstein (1879-1955) with the theory of relativity. FIGURE 4 shows Marie Curie (1867-1934) who made major contributions to both physics and chemistry with her research on radioactivity. In fact, Curie was the first woman to win a Nobel Prize and is still the only scientist to win Nobel Prizes in two different fields (Physics in 1903, Chemistry in 1911).

FIGURE 4. Marie Curie in 1903; Albert Einstein in 1921 (Nobel Foundation/Wikimedia Commons).
✔ QUICK-CHECK 5.3: TRUE or FALSE? The European Renaissance was a cultural and intellectual revolution derived from the rediscovery of Greek thought.
✔ QUICK-CHECK 5.4: TRUE or FALSE? Galileo pioneered the use of experimentation to validate observational theories, and as a result is considered by many to be the father of modern science.
The Scientific Method
The integration of experimentation into scientific inquiry, formalized by Galileo, separates modern science from the pre-science of the Greeks and Romans. Rather than just observation and contemplation, modern science requires that theories be validated by experimentation. Galileo's experimentation-based approach to science has since been codified into the scientific method, which is the accepted, common process by which modern science is conducted. The scientific method can be described in six steps (with the easy-to-remember mnemonic OHDEAR):
- OBSERVE: When trying to understand a natural phenomenon, such as the motion of planets in the night sky, the first step is to observe the phenomenon in question. For example, early humans watched the sky and noted that some lights moved differently than others, raising the question as to why they were different.
- HYPOTHESIZE: Once a phenomenon has been observed, a hypothesis is formulated as to why it behaves as it does. For example, the relative motion of the planets might lead to the hypothesis that they are bodies orbiting much closer to the earth than stars.
- DESIGN: Next, an experiment is designed to test that hypothesis. For example, a mathematical model of planetary motion, perhaps using the circular orbits proposed by Copernicus, could be developed to predict the relative motion of the planets.
- EXPERIMENT: The experiment is then conducted to either confirm or refute the hypothesis. For example, observations of planetary motion over time could be collected and compared with the predicted positions given by the model.
- ANALYZE: Once the experiment is completed, the results must be analyzed to see if they confirm or refute the hypothesis. For example, if planetary motion matched the predictions, the hypothesis would be confirmed. If not, then the hypothesis is refuted.
- REVISE: Very often, discrepancies from expectations can lead to revisions or refinements in the hypothesis. For example, recognizing that the circular model of planetary motion did not quite match observations led Kepler to revise Copernicus' model to instead use elliptical orbits. The revised hypothesis would then need to be tested by repeating the steps of the scientific method.
FIGURE 5 depicts the six steps of the scientific method as a circle, signifying that scientific inquiry often requires repetition. In the real world, the initial results of experiments often do not produce the expected results. This may be due to an incorrect or incomplete hypothesis, or perhaps a faulty design in the experiment. When unexpected results occur, the scientist must repeat the process, observing the phenomenon to see if something important was missed, perhaps revising the hypothesis and designing/conducting a new experiment. In the example described above, telescopic observations might partially match the circular model of orbits, suggesting that the model is close to correct and leading to a revised hypothesis involving elliptical orbits.

FIGURE 5. The Scientific Method (with mnemonic OHDEAR).
The scientific method is a general-purpose, robust approach to understanding phenomena across a variety of areas. For example, a botanist who observes the stunted growth of plants might hypothesize that a specific lack of nutrients in the soil is the problem, then design an experiment to compare the growth of plants in the current soil with plants in nutrient-fortified soil. Even non-scientists utilize the scientific method to understand and solve real-world problems. An automobile mechanic might observe an engine misfiring, hypothesize the cause (e.g., a bad spark plug), and design an experiment (e.g., replacing the spark plug) to test that hypothesis. Even programmers and Web designers utilize the scientific method, observing the unintended behavior of a program/page, hypothesizing as to the cause (e.g., a malformed statement), and designing an experiment (e.g., a fix to that statement) to debug it.
✔ QUICK-CHECK 5.5: TRUE or FALSE? The scientific method can only be applied to understanding phenomena in the natural sciences.
Consistency vs. Accuracy
When applying the scientific method to a problem, it is essential that the experiment produce reliable, reproducible results. That is, the experiment, when conducted under identical conditions, should produce the same results. Of course, it is difficult to ensure the exact same conditions for every experiment, so slight variations in results can be expected. For example, suppose you dropped a ball from a specific height. Newton's laws of gravity and motion make it possible to predict how long it would take to fall. In practice, tiny variations in humidity and wind might affect the exact time, but as long as most factors are controlled for, you would expect the times to be close to the same.
Consistency is a measure of how reproducible a result is. If you measured the time it takes for the ball to fall from the same height five times and those times were identical (or extremely close), you would say those results were consistent. If you obtained widely varying times, you would say the results were inconsistent and would have to question the validity of the experiment (or perhaps identify uncontrolled factors that are affecting the result). To confirm a hypothesis through experimentation, you must be able to produce consistent results under the same conditions. When a scientist publishes a new discovery, they must also publish the exact methods they used to confirm their hypothesis. If other scientists are unable to reproduce those same results, then that work will not be accepted. As science fiction author James S.A. Corey wrote: "Once is never. Twice is always." An experimental result is not meaningful if it cannot be reproduced.
A closely related measure to consistency is accuracy, or how close an experimental result is to the correct (or expected) result. For example, if theory predicted it would take eight seconds for the ball to fall and the experiment timed the ball at eight seconds (or very close to it), we would say that was an accurate result. Accuracy can only be applied as a measure when you know the expected outcome of an experiment.
To illustrate these concepts, suppose that a scientist, call her Marie, performed three different experiments with the falling ball. The timings for those experiments are as follows:
Marie's timings: 8.1 seconds 7.7 seconds 7.9 seconds
These results are fairly consistent: the largest timing (8.1 seconds) is only 5.2% larger than the smallest timing (7.7 seconds), since (8.1-7.7)/7.7 = 0.4/7.7 = 0.052 = 5.2%. Now suppose a second scientist, call him Isaac, reproduced those same experiments and obtained the following timings:
Isaac's timings: 8.1 seconds 8.3 seconds 8.2 seconds
Since these timings are closer together than Marie's, we would say that Isaac's results are more consistent. In particular, the largest timing (8.3 seconds) is only 2.5% larger than the smallest timing (8.1 seconds), since (8.3-8.1)/8.1 = 0.2/8.1 = 0.025 = 2.5%.
In the real world, experimental consistency and accuracy tend to go together. The more consistent the results of repeated experiments are, the more confident you can be that the result is accurate. Marie's timings average to 7.9 seconds, while Isaac's average to 8.2 seconds. If repeated experiments stayed close to these timings, you would feel confident in saying that the expected time for the ball is around 8 seconds. If a third scientist obtained widely varying timings, e.g., 12 seconds, 4 seconds and 10 seconds, you would be highly skeptical of those results and need to revisit their experimental design or conditions to determine where corrections need to be made.
Interestingly, if we determined that the ball should take exactly 8 seconds (based on theory), then the average of Marie's timings is more accurate than average of Isaac's timings since 7.9 is closer to 8 than 8.2 is. Consistency does not always ensure accuracy. In this case, it might be that the method of measurement (e.g., a person with a stopwatch) is not precise enough to make these discrepancies meaningful. The scientist designing the experiment must determine how consistent and/or accurate the results need to be, based on the experimental goals and the precision of the tools used. It should also be noted that consistency and accuracy may not go together if the hypothesis or experiment is flawed. For example, consider a pair of weighted dice that roll seven every time. These dice would produce consistent results (the same total every roll) but would be considered inaccurate if they were mistakenly assumed to be fair dice.
✔ QUICK-CHECK 5.6: If you repeatedly flipped a coin, you would expect to obtain HEADS (roughly) half of the time. Suppose Chris performs three different experiments, flipping a coin 100 times each and obtains HEADS 46, 50, and 54 times, respectively. Similarly, Pat performs a different three experiments, flipping the coin 100 times each and obtaining HEADS 55, 56, and 57 times, respectively. Which set of data is more consistent? Which set of data is more accurate?
Computational Thinking
While the scientific method still provides the blueprint for systematically studying and understanding phenomena, it is not directly applicable to many real-world problems. When faced with a problem such as organizing a job schedule or finding the tallest person in a room full of people, a more applied problem-solving approach is needed. As early as the 1950s, scientists and engineers recognized that computers were more than just tools for solving problems. As computer pioneer Alan Perlis noted, coding enabled a new way of reasoning about problems and designing solutions. Education researchers soon adopted the structured, logical thinking associated with computers as natural models for teaching problems solving. For example, Seymour Papert (1928-2106) and his research team at MIT developed the Logo programming language and mobile robots as tools for teaching children to reason more effectively. As Don Knuth, author of the multivolume work The Art of Computer Programming stated in 1974: "Actually, a person does not really understand something until he can teach it to a computer."
The term computational thinking was first coined in 1980 by Seymour Papert. However, it did not capture popular attention until 2006, when Jeannette Wing (FIGURE 6), the President's Professor of Computer Science at Carnegie Mellon University, wrote an influential article titled Computational Thinking. In this article, Wing defined computational thinking as "a set of problem-solving methods that involve expressing problems and their solutions in ways that a computer could also execute." She argued that computational thinking is a fundamental skill for everyone, not just computer scientists, that can readily be applied to solve many problems from everyday life.

FIGURE 6. Jeannette Wing in 2013 (World Economic Forum/Wikimedia Commons).
Since the publication of Wing's article in 2006, computational thinking has been widely recognized as an essential skill for 21st century learning (along with critical thinking, communication, collaboration and creativity). The specific characteristics that define computational thinking, however, are still not widely agreed upon, as people often focus on different aspects when describing computational thinking. Four high-level characteristics consistently emerge, however.
- DECOMOPOSITION:
- Large, complex problems can be overwhelming. An important step in solving a complex problem is breaking it down into smaller, more manageable problems. Once solutions to the smaller problems have been designed and developed, they can be combined to solve the original, larger problem.
- PATTERN RECOGNITION:
- As is the case with most endeavors, problem-solving improves with experience. Recognizing how solutions to similar problems can be applied to new problems is a powerful step for leveraging past experience and avoiding having to solve every new problem from scratch.
- ABSTRACTION:
- Complex problems often have too many details, many of which may not prove relevant to the design of a solution. Being able to abstract away irrelevant details and focus on those that are essential enables a problem-solver to develop a high-level solution, perhaps adding additional details later as needed.
- ALGORITHMS:
- The final step in solving a problem is to codify that solution as an algorithm. As you will learn in more detail in Chapter C6, an algorithm is a step-by-step sequence of instructions for carrying out some task. An algorithm might be informal, such as a recipe for baking a cake or driving directions to your house, or formal enough for a computer to carry out (i.e., a program).
We all practice computational thinking every day as we carry out tasks. When you assemble a bookcase, you DECOMPOSE the task by focusing on distinct steps in the process (e.g., unpacking the parts, identifying each part and its purpose, constructing the base, attaching the sides and top, and finally hanging the shelves). You utilize PATTERN RECOGNITION by leveraging past assembly tasks. For example, if you had previously built a different type of furniture, say a desk, then unpacking and organizing the parts can be performed in much the same way. Likewise, some of the tools used might be the same, such as a screwdriver or Allen wrench, so you already know how to use those. Using ABSTRACTION, you can focus on the important tasks, putting off details (e.g., the heights of the shelves, the location of the bookcase along the wall) and focus on the basic assembly. Finally, you would like to remember the steps you took during the assembly process so that you could recreate that process the next time you need to assemble a bookcase. You might do so by writing down a detailed sequence of instructions (i.e., an ALGORITHM) that you could follow, or even better, could give to a friend so that they could benefit from your experience. Of course, most furniture manufacturers will do this for you, providing printed instructions that you can follow as opposed to having to invent the assembly algorithm yourself.
As you will learn in the Explorations section of this book (Chapters X1-X10), computers are powerful tools for solving many real-world problems. If you need to calculate your grade in a class or simulate compound interest on an investment, a computer program can be designed and executed to solve these types of problems. In these cases, the computational thinking process culminates in an algorithm written as a program, which can be understood and automatically executed by a computer. The exercises you will complete in those chapters, as well as the end-of-chapter projects you will design and implement, will take you through the entire computational thinking process, starting with problem specifications and ending with executable programs.
✔ QUICK-CHECK 5.7: TRUE or FALSE? Decomposition refers to the ability to ignore irrelevant details and focus on those aspects of a problem that are essential to designing a solution.
✔ QUICK-CHECK 5.8: TRUE or FALSE? An algorithm is a step-by-step sequence of instructions for carrying out some task.
Example: Finding the tallest person in a room
Before considering more software-oriented examples of computational thinking in later chapters, it is worthwhile to consider another real-world example. The following example, finding the tallest person in a room, is complex enough to require a careful approach to devising a solution using the characteristics of computation thinking. It also demonstrates that computational thinking can often take multiple paths, leading to different algorithms that solve the same problem. Methods for evaluating different solutions to the same problem will be described in Chapter C6.
Suppose you are in a room full of people and (for whatever reason) wish to identify the tallest person in the room. At first glance, this problem seems relatively straightforward to comprehend. The initial condition is a room full of people. The goal is to identify the tallest person. However, deeper issues must be explored before a solution can be proposed. For example, how do you determine how tall a person is? Can you tell someone's height just by looking at them or do you need to measure them? If you ask someone their height, will they tell the truth? What if there is more than one tallest person (i.e., if two individuals are the exact same height)?
- DECOMOPOSITION:
- The first step in solving this problem is to break it down into smaller, more manageable tasks. To complete this task, one thing we will have to be able to do is determine an individual's height. This could be accomplished just by asking them (and assuming they tell the truth) or perhaps measuring them using a tape measure. We will need to make sure that we check each person in the room, hopefully without duplication, so that we don't miss anybody. Finally, we will need some way to keep track of the tallest person, perhaps by entering names and heights in a notebook or on a tablet.
- PATTERN RECOGNITION:
- At this point, we might consider past problems that have been solved and any insights they might provide. For example, we might note that in past experiences dealing with large groups, it has proven useful to organize the people before beginning a task. As a result, we might start by having the people all line up along a wall, so it will be easier to compare their heights without risking missing someone. We might also recall past uses of a pad of paper and pencil and recognize their applicability here. At this initial stage of planning, we might also recognize that the task of asking someone their name and height is going to be repeated many times. Once we determine the optimal way to do this, we can apply that same action over and over.
- ABSTRACTION:
- In any real-world task, there are many details that are not relevant to a solution. For this problem, we don't care about the gender, hair color, or favorite movie of each person — all we want to do is determine the name and height of the tallest person. But what exactly does it mean to be tallest? If two people report as being 5'10", do we consider them the same height or do we care about fractions of an inch? To keep things simple, let us assume that we don't care about fractions, so if two people are both 5'10", we consider them the same height. If there is more than one tallest person, finding any one of them is acceptable.
- ALGORITHMS:
- Equipped with our new understanding of the problem, we are prepared to devise a step-by-step solution:
Finding the tallest person in a room (Algorithm 1):
- Line up all the people along one wall.
- Ask the first person to state their name and height, then write this information down on a piece of paper.
- For each successive person in line:
- Ask the person their name and height.
- If the stated height is greater than the height written on the paper, cross out the old information and write down the name and height of this person.
- When you have reached the end of the line, then the name and height of the tallest person will be written on the paper.
To see how this algorithm works, we can carry out the steps on a fictitious group of people (FIGURE 7). Initially, you write down the name and height of the first person (Chris, 5'8"). Working your way down the line, you ask each person for their height and update the page when greater height is encountered (first Charles, 5'11"; then Jack, 6'0"). When you reach the end of the line, the name and height of the tallest person (Jack, 6'0") is written on the paper.
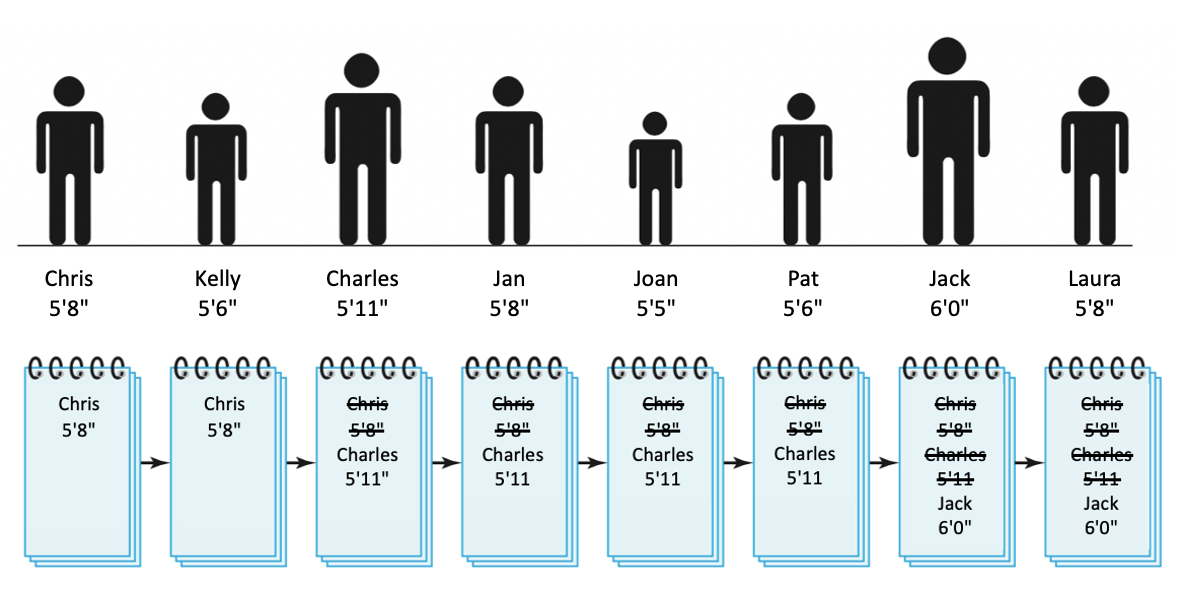
FIGURE 7. Algorithm 1 for finding the tallest person.
This algorithm is simple, and it's easy to see that it would work on any group of people. Because you go through the entire line, every person is eventually asked their height. When you reach the tallest person, their height will be greater than the height currently on the paper. And once you write the tallest person's information down, it will stay on the paper, as no one taller will be found.
Algorithm 1 effectively locates the oldest person in the room. However, this problem — like most — can be solved many ways. For example, many problems dealing with large groups can be tackled using decomposition. That is, the large group is divided into smaller groups, the task is applied to those smaller groups, and the results of those tasks are combined to produce the answer for the entire group. In this case, we could pair off the people and simultaneously determine the tallest person in each pair. In the time it takes for each pair to compare heights, half of the people could be eliminated, and the process can then be repeated until the tallest person is located:
Finding the tallest person in a room (Algorithm 2):
- Line up all the people along one wall.
- As long as there is more than one person in the line, repeatedly:
- Have the people pair up (1st and 2nd in line, 3rd and 4th in line, and so on). If there is an odd number of people, the last person will remain without a partner.
- Ask each pair of people to compare their heights.
- Request that the shorter of each pair leave the line.
- When there is only one person left in the line, that person is the tallest.
Algorithm 2 is slightly more complex than Algorithm 1 but has the same end result — the tallest person in the room is located. In the first round, each pair compares heights, and the shorter of the two partners subsequently leaves the line. Thus, the number of people in line is cut roughly in half (if there is an odd number of people, the extra person will remain). The remaining people then repeat this process, reducing the size of the line each time. Eventually, the number of people in line drops to one. Clearly, the tallest person cannot have left, because they would have been taller than any potential partner in the line. Therefore, the last person remaining is the tallest. FIGURE 8 demonstrates performing this algorithm on the same eight people used in FIGURE 7. In three rounds, the line of people shrinks until it contains only the tallest person.

FIGURE 8. Algorithm 2 for finding the tallest person.
The advantage that Algorithm 2 has over Algorithm 1 is that it will be faster on large groups of people. Suppose it takes 10 seconds to ask and potentially write down a person's name and height. Algorithm 1 requires asking each person their height, so a room with 8 people requires 10 x 8 = 80 seconds, 16 people would require 10 x 16 = 160 seconds, 32 people would require 10 x 32 = 320 seconds, and so on. Doubling the number of people doubles the time required. With Algorithm 2, each round requires the time for two people to state and compare their heights, again let's say that also takes 10 seconds. Since a room of 8 people only requires 3 rounds, the tallest person can be found in 10 x 3 = 30 seconds. Furthermore, doubling the number of people in the room only requires one additional round, so 16 people would require 10 x 4 = 40 seconds, 32 people would require 10 x 5 = 50 seconds, and so on. In a large lecture hall with 400 people, the difference is dramatic: Algorithm 1 would require 10 x 400 = 4,000 seconds (more than an hour), whereas Algorithm 2 would require only 10 x 9 = 90 seconds (a minute and a half).
When faced with the task of finding the tallest person in a room, most people would come up with a variation of Algorithm 1. The development of Algorithm 2 requires considerable experience solving problems, which enables the algorithm designer to recognize a useful approach (PATTERN RECOGNITION) and a corresponding way of breaking down the task (DECOMPOSITION). This is an important characteristic of computational thinking — the more problems a person solves, the more experience they can build from. This means that an experienced problem-solver can draw on patterns from previously solved problems and can more effectively divide large problems based on those past solutions. Like most endeavors, the more practice you have at computational thinking, the better you get at it!
✔ QUICK-CHECK 5.9: TRUE or FALSE? For a precise, clearly stated problem, there can be only one algorithm that provides a solution.
✔ QUICK-CHECK 5.10: Suppose it took 5 minutes to find the tallest person in a room of 50 people using Algorithm 1. How long would it take to find the tallest person if there were 100 people?
Chapter Summary
- Science is "a system of knowledge covering general truths or the operation of general laws especially as obtained and tested through scientific method." (Merriam Webster).
- Modern science traces its roots back to the natural philosophers of ancient Greece (such as Thales, Plato, and Aristotle), who used contemplation and observation to develop theories of the natural world.
- During Europe's "Dark Ages," Greek science was preserved and advanced by Arab scholars throughout parts of Europe, northern Africa, the Middle East, and eastern Asia.
- The European Renaissance (14th-16th centuries) was a cultural and intellectual revolution that was derived from the rediscovery of Greek thought, and encompassed widespread political reform, artistic expression, and the rise of humanism.
- The Scientific Revolution of the 16th-17th centuries led to a world view in which the universe was thought of as a complex machine that could be understood through careful observation and, more importantly, experimentation.
- Galileo pioneered the use of experimentation to validate observational theories, and as a result is considered by many to be the father of modern science.
- Galileo's experimentation-based approach to science has since been codified into the "scientific method," whose six steps are Observe, Hypothesize, Design, Experiment, Analyze and Revise.
- Consistency is a measure of how reproducible a result is. For a scientific work to be accepted, it must be reproducible (i.e., produce consistent results under identical conditions).
- Accuracy is a measure of how close an experimental result is to the correct (or expected) result.
- Computational thinking is an approach to problem-solving that involves expressing problems and their solutions in ways that a computer can execute.
- Four high-level characteristics of computational thinking are Decomposition (breaking a complex problem into smaller, more manageable problems), Pattern Recognition (recognizing how solutions to similar problems can be adapted to solve new ones), Abstraction (ignoring irrelevant details and focusing on those features that lead to a solution), and Algorithms (representing the solution as a step-by-step sequence of instructions).
- Computational thinking can often take multiple paths, leading to different algorithms that solve the same problem.
Review Questions
- TRUE or FALSE? The steps of the scientific method are Decomposition, Pattern Recognition, Abstraction, and Algorithms.
- TRUE or FALSE? Accuracy is a measure of how close an experimental result is to the correct (or expected) result.
- TRUE or FALSE? A sequence of instructions for assembling a bookcase does not qualify as an "algorithm," as the instructions are not written in formal, mathematical notation.
- The scientific method is the common process by which modern science is conducted. Describe the key steps in the scientific method.
- Describe one example of how a biologist might apply the scientific method to solving a problem in the biological sciences.
- Describe one exercise or lab from this class in which you utilized the scientific method in solving a problem.
- Describe a real-world example where you have used computational thinking to solve a problem. Be sure to mention how any of the computational thinking characteristics (decomposition, pattern matching, abstraction, and algorithms) applied to the development of your solution.
- Consider Algorithm 1 for finding the tallest person in a room. If it takes 20 seconds to ask and write down a person's name and height, how long would it take to find the tallest person in a room of 10 people? 20 people? 100 people?
- Consider Algorithm 2 for finding the tallest person in a room. If it takes 20 seconds for a round (a pair of people comparing heights and the shorter sitting down), how long would it take to find the tallest person in a room of 10 people? 20 people? 100 people?
- Suppose that you were asked to arrange a group of people in sequence from shortest to tallest. In other words, you must organize a line that begins with the shortest person and continues in increasing order according to height. Describe an algorithm for completing this task.
